パスカルの三角形とは?
(a+b)n (n:整数) について、展開(カッコを外す)をしてみましょう。
- n=1 のとき (a+b)1=a+b
- n=2 のとき (a+b)2=a2+2ab+b2
- n=3 のとき (a+b)3=a3+3a2b+3ab2+b3
- n=4 のとき (a+b)4=a4+4a3b+6a2b2+4ab3+b4
という感じです。ところで、たらたら書きましたが、別に計算したわけではなく、覚えているわけでもありません。
例えば、(a+b)3に注目してみましょう。改めて、展開式を以下のように書いてみます。
(a+b)3=a3+3a2b+3ab2+b3 = a3b0 + 3a2b + 3ab2 + a0b3
展開後の a に注目すると a3 a2 a1 a0 と並んでいます。
展開後の b に注目すると b0 b1 b2 b3 と並んでいます。
3から始まるのは、(a+b)3 が3乗になっているからです。
あとは係数の(1,3,3,1)が問題です。これが、パスカルの三角形の一部になります。先ほどの展開式から、係数だけを抜き出してみましょう。
1 1
1 2 1
1 3 3 1
1 4 6 4 1
ですが、次のように見てみると、ホホー、です。
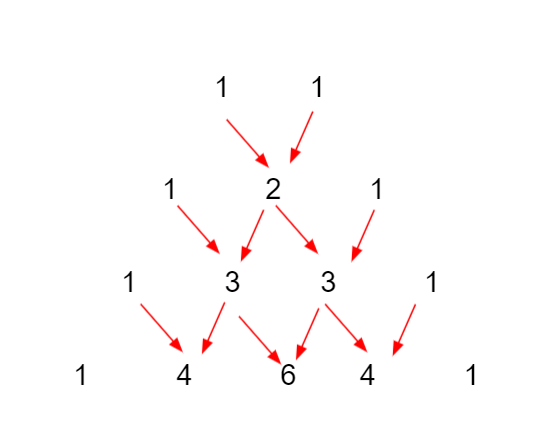
三角形の両端はつねに1です。それから、矢印の根っこの数値を足すと、矢印の先の数値になっています。これをパスカルの三角形といいます。ここでは4段目で止めていますが、これは無限に続きます。
pyhtonでパスカルの三角形を作ってみよう
pythonで組んでみましょう。
pa=[] pa.append(1) pa.append(1) for i in range(0,5,1): #print out print(str(pa)) #make pascal nagasa=len(pa) pa1=[] pa1.append(1) for j in range(0,nagasa-1,1): pa1.append(pa[j]+pa[j+1]) pa1.append(1) pa=pa1 del pa1
【プログラムを見てみよう】
paにパスカルの三角形を作っていきます。何か所か pa.append(1) があります。これはパスカルの三角形の端っこの1をいれています。
len(pa)はpaの長さを示しています。例えば、pa=[1,3,3,1]であれば、4つの要素がありますから、len(pa)=4になります。
パスカルの三角形のpaの次の段をpa1に入れています。
pa=pa1 で、pa1の結果をpaに上書きしています。
役目の終わったpa1は del pa1 で消去しています。
for 文を二重に使っていますので、for i の中で回す for文はわかりやすくするために for j とでもしておきます。
結果を見てみましょう。
[1, 1]
[1, 2, 1]
[1, 3, 3, 1]
[1, 4, 6, 4, 1]
[1, 5, 10, 10, 5, 1]
パスカルの三角形の5段目までを作ることができました。
これでxnの微分が計算できそう
xnの微分は、
{ (x+h)n-xn }/h
を計算して hを0に限りなく近づけることで求めることができます。ここで、(x+h)n を求めないといけないですが、この場合は全部求める必要はないです。どういうことか見ていきましょう。
(x+h)n =xn+nxn-1h+axn-2h2+(h3、h4・・・を含む項につき、以下省略)
まず赤いnはですが、これは(x+h)n のnと同じ値になります。
次にaですが、この値は計算可能なのですが、hを0に近づける過程で、この項以降は落ちるので、このままaとしておきまます。
(x+h)n - xn =nxn-1h+axn-2h2+(以下省略)
から、
{(x+h)n - xn } / h=nxn-1 +axn-2h+(hを含む項につき以下省略)
なので hを0に近づけると
lim {(x+h)n - xn } / h=nxn-1
になります。なんとなれば、hを含む項は、0に近づくからです。
なので、
(xn)’=nxn-1
となります。ダッシュは微分を表しています。
pythonで微分を計算してみよう
f(x)=x6 でx=3のとき、微分した値をpythonで求めてみましょう。
まず理論を計算しておきます。
f(x)=x6 なので、
f'(x)=6x5
なのでx=3のとき、
f'(3)=6(3)5=1458
になります。ではpythonで実験値を求めてみましょう。
import math h=1 for i in range(0,5,1): a=( math.pow(3+h,6)-math.pow(3,6) )/h print(str(a)) # h renew h=h*0.1
【プログラムを見てみよう】
(3+h)6 はプログラムでは、math.pow(3+h,6) と書くことができます。ですので、微分は、
( math.pow(3+h,6)-math.pow(3,6) )/h
をhの値をどんどん小さくしていくことで、微分値の近似値(近い値)を求めることができます。結果を見てみましょう。
3367.0
1585.0368100000014
1470.2041351800628
1459.2155401348914
1458.1215054033687
5回目の計算で、理論値に近い値が出ています。
さらに学習したい方に
ずぶの素人です系の方は
Pythonの絵本 Pythonを楽しく学ぶ9つの扉 [ 株式会社アンク ]
他の言語はかじりました系の方は



コメント