微分の定義を確認しよう
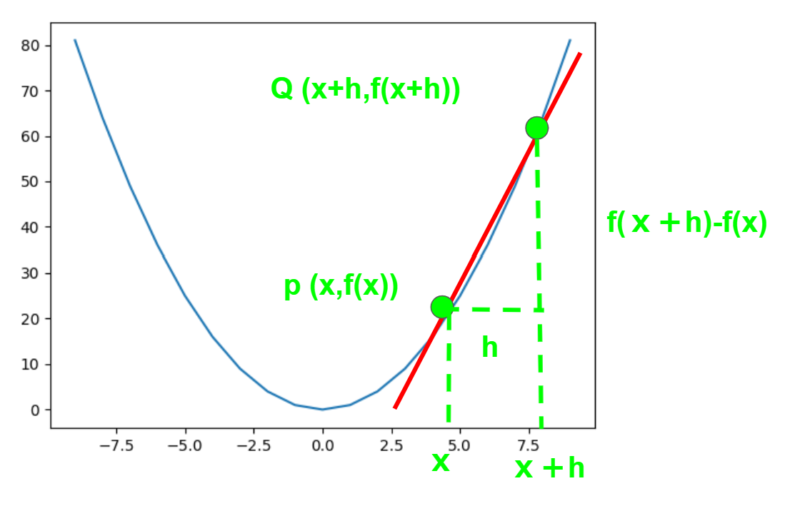
前回のコラムを読んでいただいた方には、もう簡単な内容です。下の図を見てみましょう。y=x2のグラフを書いています。
関数は、前回y=x2と書いたのですが、
f(x)=x2
と書くこともあります。”fは変数xの関数ですよ”と強調しています。さて、x座標がxのときのポイントP(x,f(x))と、x座標がx+hのときのポイントQ (x+h,f(x+h))をとります。で、例のごとく、P点での傾き(接線)を求めてみましょう。
まず、2点P,Qを通る線の傾きを求めます。
傾き=yの増加量 / xの増加量
={ f(x+h)-f(x) } / { (x+h)-x } = { f(x+h) – f(x) } / h
hを0に限りなく近づければ、PQを結ぶ線は、Pでの接線に近くなります。ここで前回のリミットを思い足すと、
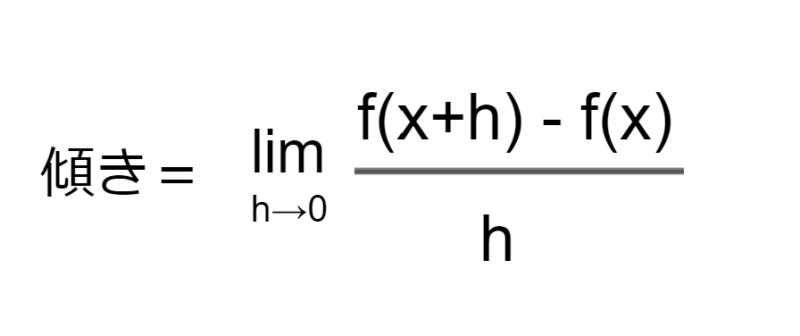
になります。この傾きを、f'(x)と書いて、f(x)の微分といいます。改めて書けば、
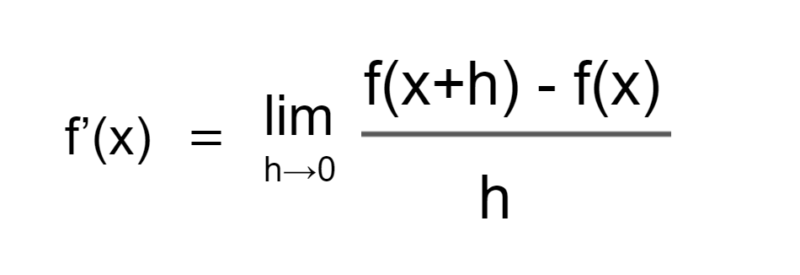
になります。
f(x)=x3の微分を求めてみよう
x=5で微分した値を、理論とpythonを使った実験から求めてみましょう。
【理論値】
f(x)=x3
から、
f'(x)=lim { (x+h)3-x3 } / h
=lim{ (x3+3x2h+3xh2+h3) – x3} / h
=lim (3x2h+3xh2+h3) / h
=lim ( 3x2+3xh+h2 )
=3x2 (なんとなれば、hは限りなく0に近いので、3xh=h2=0とみなせる)
なので、x=5を代入すれば、
f'(5)=3×52=75
になります。
【pythonで実験してみよう】
プログラムを見てみます。
h=1
for i in range(0,5,1):
atai=( ((5+h)*(5+h)*(5+h)-5*5*5)/(5+h-5) )
h=h*0.1
print('h='+str(h)+'のとき、f(x)='+str(atai))atai に、微分の値が入ります。
for文をくり返すごとに、hの値は0.1倍になっていきます。ここでリミットのような演算を表現しています。
print()で結果を打ち出しています。
print(‘h=‘+str(h)+’のとき、f(x)=‘+str(atai))
青い部分は数値を打ち出します。赤は固定な文字列なので、’ ’ でくくります。そしてその間は+で結びます。これでちょっと見栄えが良くなります。
h=0.1のとき、f(x)=91.0
h=0.010000000000000002のとき、f(x)=76.51000000000009
h=0.0010000000000000002のとき、f(x)=75.15009999999923
h=0.00010000000000000003のとき、f(x)=75.0150010000004
h=1.0000000000000004e-05のとき、f(x)=75.00150001010724
結果は75に近い値が出ていて、理論値とあっていることが確認できました。
何が出たかというと、x=5での接線の傾きは75ですよ、ということでした。
f(x)=xn (nは整数) のときのf'(x)は?
f(x)=xnのとき、
f'(x)=nxn-1
になります。証明はまた今度取り上げましょう。どうしてかというと、(x+h)nの展開のところで、パスカルの三角形の話をしないといけないのですが、量が多くなりますので、また今度にしましょう。
さらに学習したい方は
他のプログラム言語はかじりました系の方は
今からpythonを始めます系の方は



コメント