pythonで曲線で囲まれる面積の計算をさせてみよう

pythonで曲線で囲まれた面積を計算するには？

例えば長方形の面積を出すには、縦×横で計算すればいいのですが、曲線に囲まれた面積を出すのはどうしたらいいでしょうか。y=x²のグラフを例として見てみましょう。

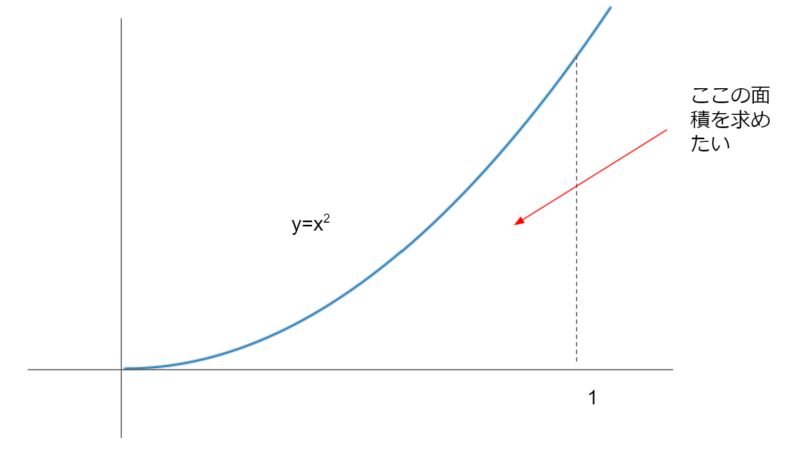
y=x²のグラフと、ｘ軸と、ｘ＝１の直線（点線部分）で囲まれた面積を求めることを考えてみましょう。ところで、長方形の面積は簡単に出せました。なので、この曲線で囲まれた部分が、なんとかして長方形に置き換えらえないものか、ということを考えます。

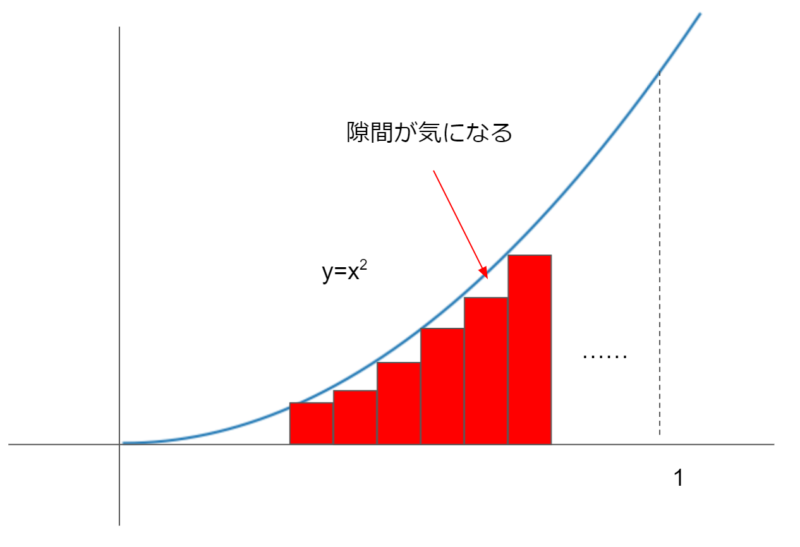
このような感じで、曲線の内部を長方形に置き換えていけば、赤い部分の面積が計算できます。ただ気になるのが隙間の部分です。これは、赤い短冊の間隔を小さくすれば、隙間も小さくなるのですが、なくなることはないです。ならば、ということで、下のように短冊をとってみましょう。

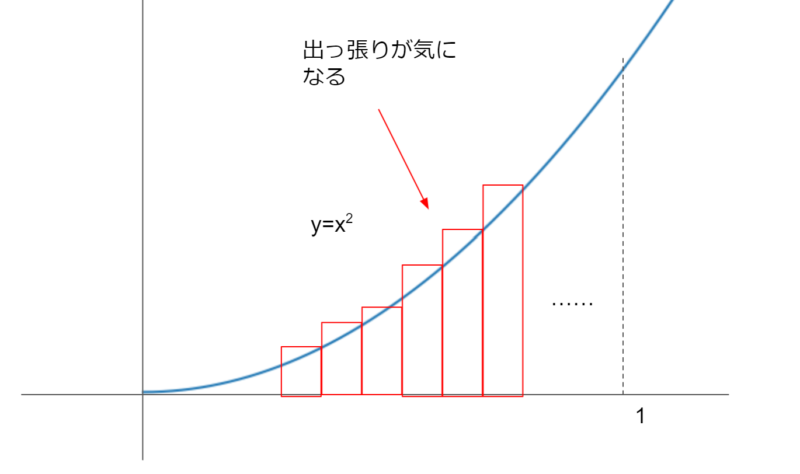
今度はでっぱりが気になります。赤い短冊の間隔を小さくしても、でっぱりの量は少なくなるのですが、なくなることはないです。

ですが、曲線部分の面積は、この２つの間にあるわけですから、間隔をどんどん小さくしながら、２つの面積を計算して、間をとればいい、ということになります。

人間が計算すると禿げてしまうのですが、pythonに実行させると、pyhtonは禿げないです。

まず、短冊が曲線より下の場合を考えてみましょう。

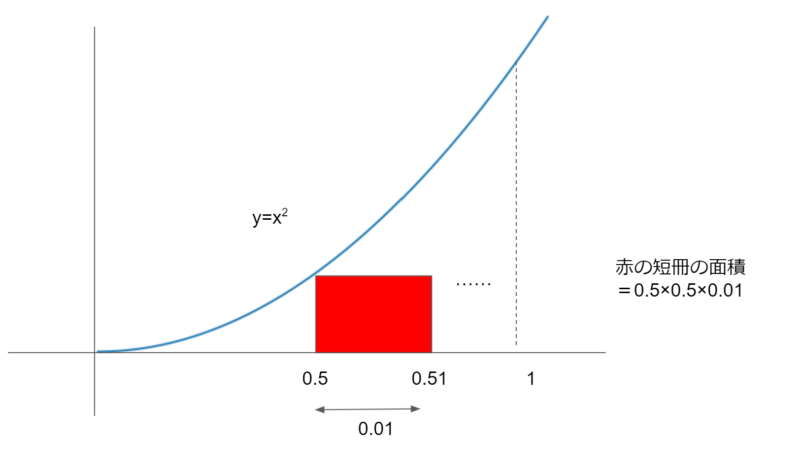
例として、0.01間隔で短冊を作成したもののうち、ｘ座標が0.5から始まる短冊を見てみましょう。この面積は、x²×0.01=0.5×0.5×0.01になります。これを0から1未満の間で計算します。

x=0
step=0.01
menseki=0

for i in range(0,100,1):
    menseki=menseki+x*x*step
    x=x+step
    
print(str(menseki))

【プログラムを見る】

xには、短冊のｘ座標の値、stepには短冊の幅を入れます。step=0.01に設定しましたので、x軸の0から１の区間は１００分割されます。ですので、１００回for文を回します。

mensekiに計算した短冊の面積を足し合わせていきます。

最後に結果を打ち出します。実行して０．328位の値になっていればOKです。

次に、短冊が求める面積より大きい場合を考えてみましょう。

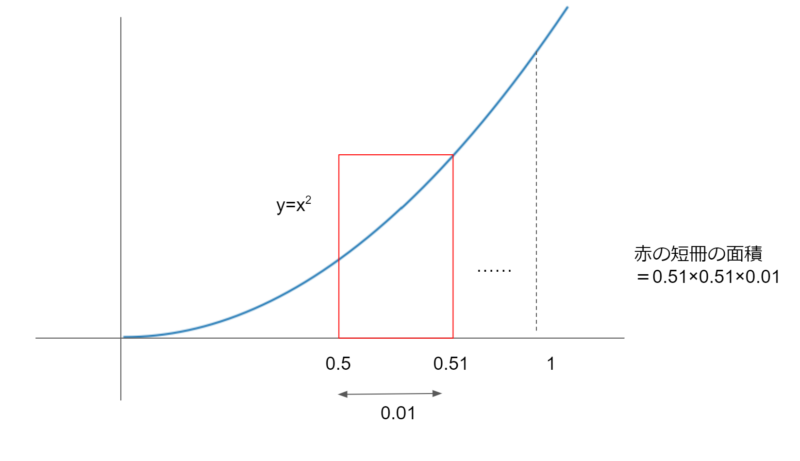
この場合の短冊の面積は、0.51×0.51×0.01です。これを踏まえて、プログラムを見てみましょう。

x=0
step=0.01
menseki=0

for i in range(0,100,1):
    menseki=menseki+(x+step)*(x+step)*step
    x=x+step 
   
print(str(menseki))

注意点は、面積を出すところで、(x+step)*(x+step)*step と変わっていることろです。実行結果は０．３３８と出ました。

ということで、

0.328<曲線の面積<0.338

ということがわかりました。短冊の幅を０．０１にして計算しましたが、短冊をもっと細かく取ればどんどん曲線の面積がしぼれてきます。

ちなみに曲線の面積の真の値は、1/3です。今後機会があれば、積分計算で取り上げてみます。