波の強さ(振幅とは?)
コサイン波の強さ(振幅)とは、波がどれだけの振れ幅で上下に揺れているか?、ということになります。例えば、
cos(2πmt) (π:円周率、m:周波数、t:時刻)
というコサイン波は、赤点線に注目すれば±1の範囲で揺れています。
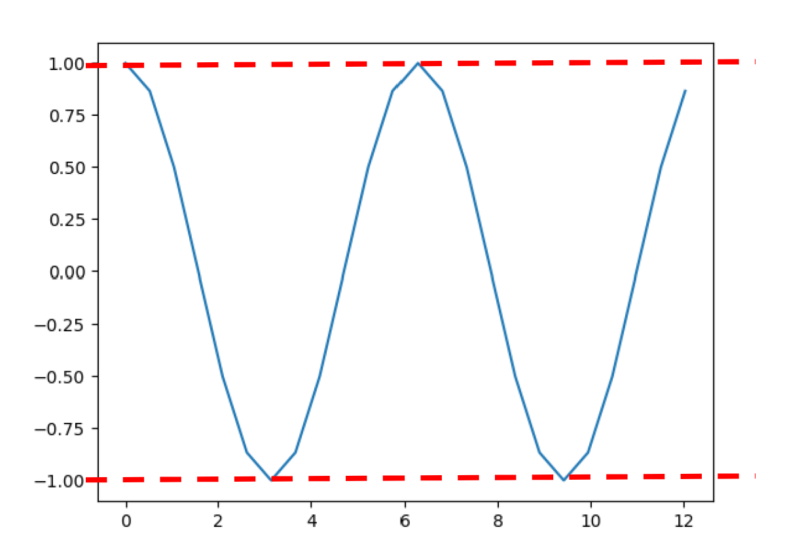
例えば振れ幅±3のコサイン波を作りたいときは、
3cos(2πmt) (3:振幅、π:円周率、m:周波数、t:時刻)
のように書きます。
pythonで確認してみよう
実際にコードを書いてみましょう。
import math import matplotlib.pyplot as plt pi=math.pi jikan=[] cos_1_atai=[] cos_3_atai=[] t=0 while t<2: jikan.append(t) sita=2*pi*t cos_1_atai.append(math.cos(sita)) cos_3_atai.append(3*math.cos(sita)) t=t+0.002 plt.plot(jikan,cos_1_atai,label='cos_1') plt.plot(jikan,cos_3_atai,label='cos_3') plt.legend(loc='lower left') plt.show()
【コードを見てみよう】
jikan=[]は、数値を入れる空のボックス(配列)を用意しています。append(数値)を使って、数値を順番に配列にとりこんでいきます。
振幅が3のコサイン波は、3*math.cos(sita) と書けます。
print()中にあるlabelの設定は、図の凡例を出すのに使います。凡例があると、どのグラフがどの線か判断しやすいですよ。
では結果を確認しましょう。
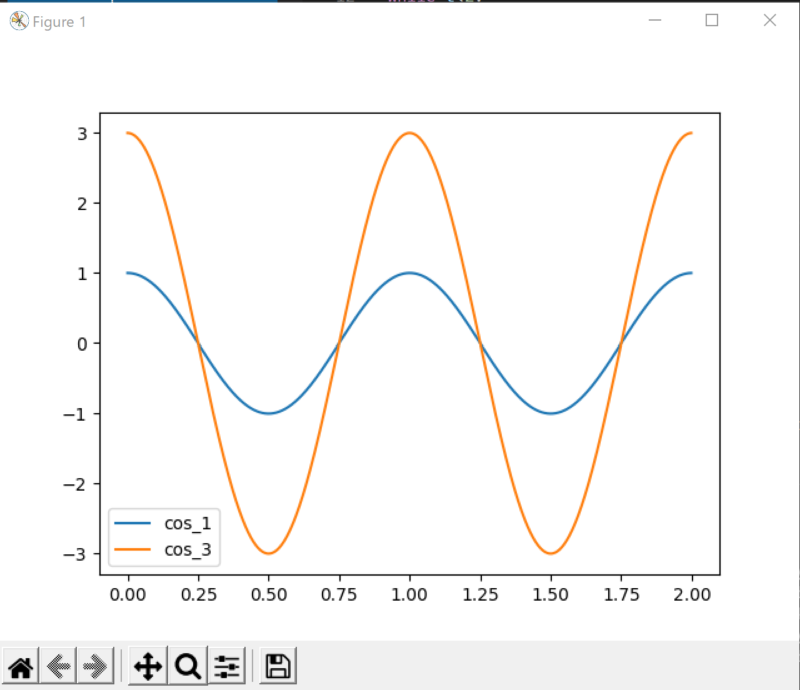
異なる周波数のコサイン波を足し合わせてみよう
異なる周波数のコサイン波を足し合わせる、は次のような計算をしてきます。
cos(2πt)+cos(4πt)+cos(6πt) (π:円周率、t:時刻)
のような足し合わせになります。ちなみに、
cos(2πt)は周波数1のコサイン波、
cos(4πt)は周波数2のコサイン波、(なんとなれば2π2t=4πt)
cos(6πt)は周波数3のコサイン波、(なんとなれば2π3t=6πt)
コードを見てみましょう。
import math import matplotlib.pyplot as plt pi=math.pi jikan=[] cos_atai=[] t=0 while t<2: jikan.append(t) sita=2*pi*t cos_atai.append(math.cos(sita)+math.cos(2*sita)+math.cos(3*sita)) t=t+0.002 plt.plot(jikan,cos_atai)plt.show()
【コードを見てみよう】
異なる周波数のコサイン波は
math.cos(sita)+math.cos(2*sita)+math.cos(3*sita)
と表現してあります。結果を確認してみましょう。
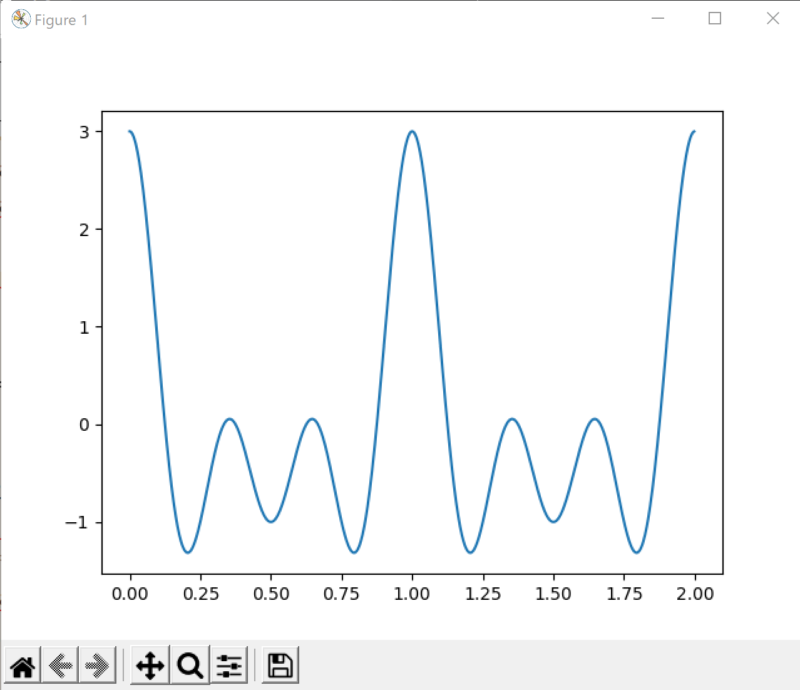



コメント