サインを見てみよう
前回コサインを見てみましたので、サインも同じくやってみます。以下のコードを保存して実行します。
import math pi=math.pi a=math.sin(0) print(str(a)) a=math.sin(pi/2) print(str(a)) a=math.sin(pi) print(str(a)) a=math.sin(pi*3/2) print(str(a))
【解説します】
前回確認したコサインとほとんど同じですが、今度はサインになっています。なので、pi(rad)のサインの値が知りたければ、
a=math.sin(pi)
でaにsin(pi)の値を取り込み、print(str(a)) で打ち出します。実行結果は、
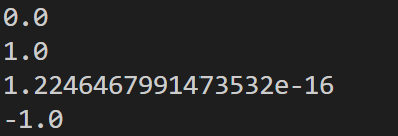
になります。1.224e-16=1.224×10-16で、限りなく0に近いので、0とみなします。単位円で見て、プログラムの実行結果が正しいかどうか確認してみましょう。今度はサインですので、下の図で緑点、紫点、青点、茶点の順番に、y座標の値を拾っていけばいいことになります。
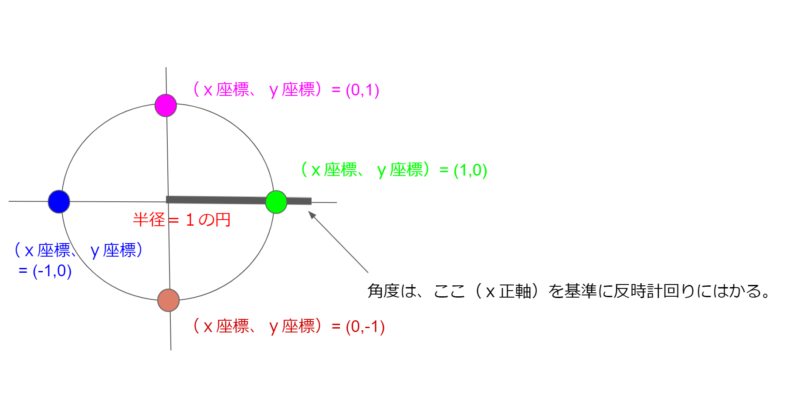
y座標は 0、1、0、-1 になり、プログラムの実行結果とあっていることが確認できました。
30°毎にコサインの値を計算してみよう
角度 0°、30°、60°、90°、120°、150°、180°、210°、240°、270°、300°、330° のコサインを計算しようと思うのですが、これをいちいち書くのはめんどくさい。なので、便利な構文を導入します。
【for文についてみてみよう】
プログラムでよくやる計算に、似たような計算を繰り返し実行する、というものがあります。いくつかやり方があるのですが、ここではfor文を取り上げてみます。次のfor文を見てみましょう。
for i in range(0,360,30): print(str(i))
まず1行目、for から始まる行ですが、これは i を 0から360未満の間で、30毎に増加させなさい、という意味になります。
2行目は、i にどのような数値が入っているか確認するため、i の値を打ち出しています。イメージは次のような感じです。

- まず i に0が入る、そして紫の部分を実行する。
- 終わったら i の値に30を足して、0+30=30にして、紫の部分を実行する。
- 終わったら i の値に30を足して、30+30=60にして、紫の部分を実行する。
- 終わったら i の値に30を足して、60+30=90にして、紫の部分を実行する。
- …
- 終わったら i の値に30を足して、300+30=330にして、紫の部分を実行する。
- 終わったら i の値に30を足して、330+30=360になるけど、i は360未満の数値なので、ここでこの繰り返しの計算は終了する。
あと一つ重要なのは、for文の中で実行したい命令は、字下げして書きます。for 文中でprint()を繰り返し実行しますが、以下のようにキーボードのTabキーを1回押してからprint()を書きます。
for i in range(0,360,30):
(tabキー) print(str(i))実行結果を見てみましょう。
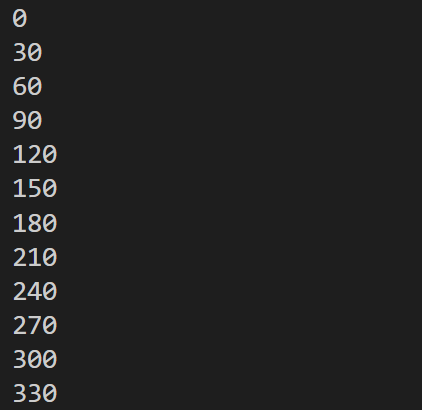
ではfor文を使って、コサインの値を計算してみましょう。
import math pi=math.pi for kakudo in range(0,360,30): kakudo_rad=kakudo*pi/180 print(str(math.cos(kakudo_rad)))
【プログラムを確認しよう】
1行目 import math は、円周率の値を得るのと、コサインの値を得るときにも必要です。
2行目 pi=math.pi でpi に円周率を取り込みます。
3行目 の空白 はあるとみやすくないですか? 空白行は入れなくてもいいです。が、ご自分が見やすくなるように工夫します。
4行目 for 文です。i のところをkakudo に変えました。これで、kakudoに 0から330までの値が30刻みで入ります。
5行目 kakudo は度で入っているので、radに直します。180°=π(rad)でした。なので、kakudo(度)が X(rad)だったとすると、
- 180°=π(rad)
- kakudo(°)=X(rad)
をたすき掛けにして、180°×X=π×kakudo から、X=kakudo*π/180 (rad)になります。
6行目で打ち出します。math.cos()は数値ですので、そのままprint()では使えません。なので、print(str(math.cos(kakudo_rad)))
のようにstr()でくくります。実行結果を見てみましょう。
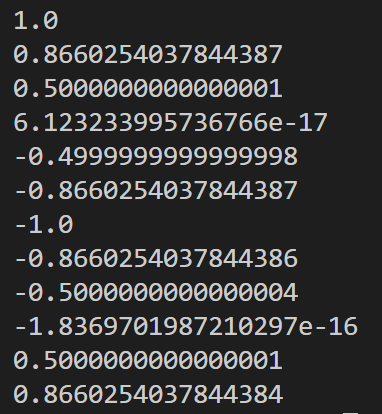
単位円を使って確認しよう
30°、60°のコサインは簡単に計算できます。コサイン30° を計算したい場合、正三角形を半分に割ってみると、30°、60°、90°の直角三角形ができます。
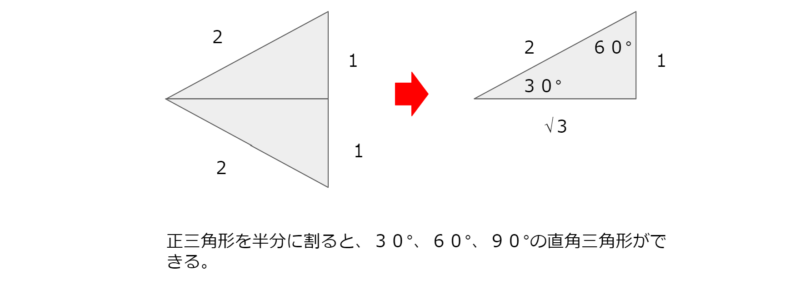
斜辺(2のところ)を計算上(単位円にあてはめたいので)1にします。なので、辺の長さをすべて半分にします。

これでコサイン30°は [√3/2 ] と出るのですが、あとあとのため単位円にあてはめます。
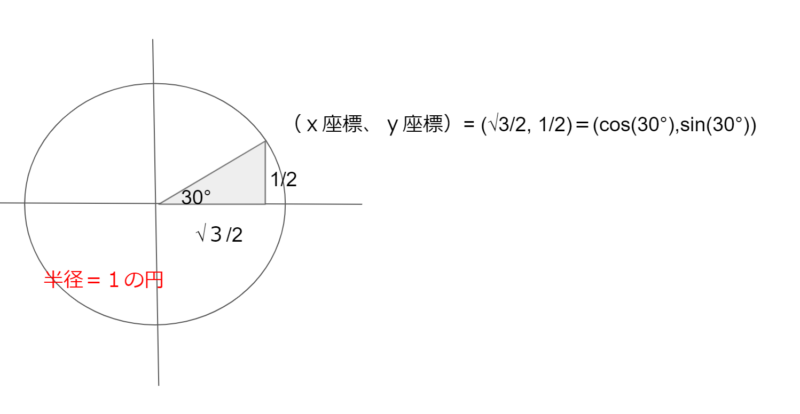
これでcos(30°)=√3/2であることが確認でました。コサイン60°の場合は、次のようの直角三角形をあてはめます。
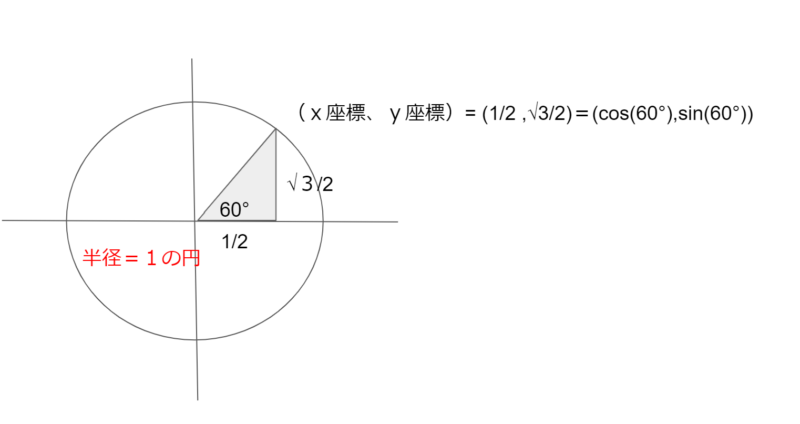
この図からコサイン60°の値は、1/2 ということがわかります。
次に120°、150°のコサインを求めたいのですが、これは30°、60°のコサインから出すことができます。
例えば150°の場合、150°の円周上のポイントは、30度のポイントのy軸を基準にして対称になっています。
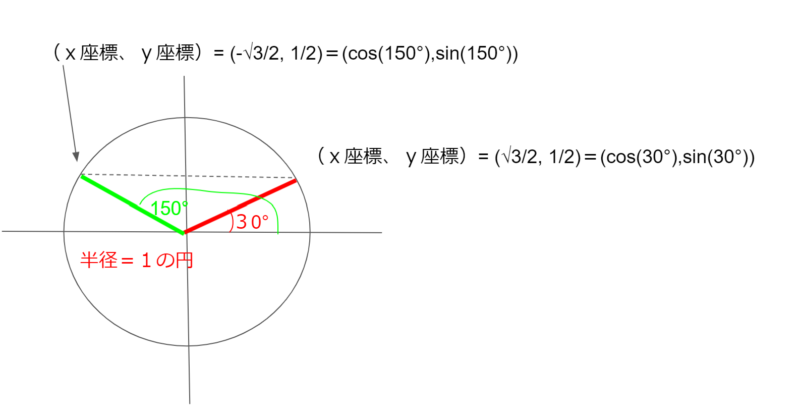
で、x座標を拾うと、cos(150°)=-√3/2になります。コサイン120°もコサイン60°を使うと簡単にもとまります。察しの良い方は、頭の中でcos(120°)=-1/2が出ていると思います。
60°の円周上の点を、y軸を対称にしてポイントを取ると、120°のポイントになります。
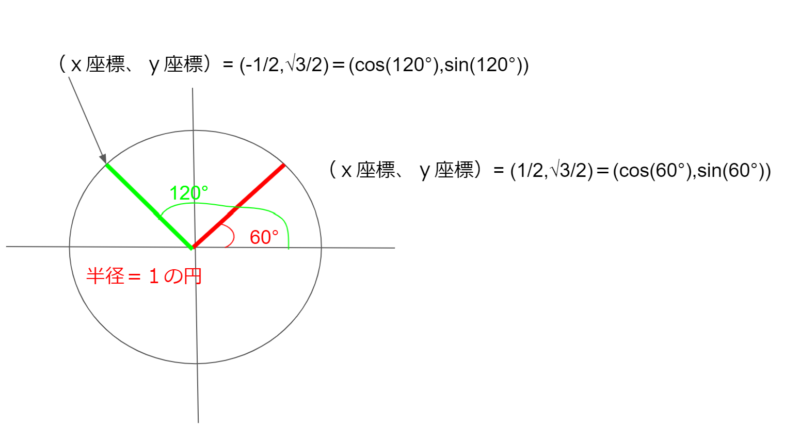
cos(120°)=-1/2 になることがわかります。
210°から330°のコサインは、今までのポイントを、今度はx軸を対称にしたポイントでみることができます。
60°、120°のポイントをx軸を対称にしてポイントを取ると、240°、300°のポイントを取ることができます。
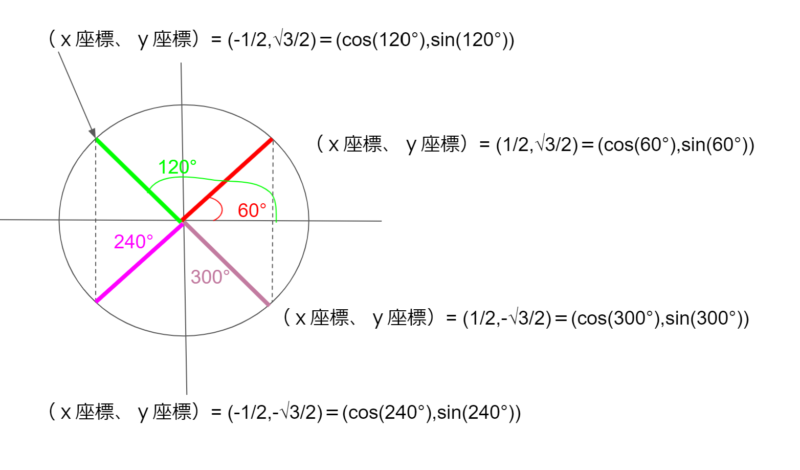
この図から、cos(240°)=-1/2、cos(300°)=1/2 であることがわかります。
最後にもう一つ。
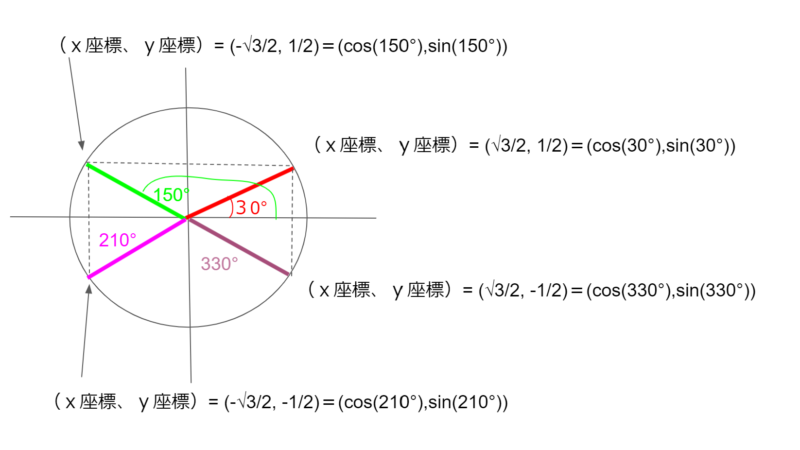
同じ要領で、cos(210°)=-√3/2、cos(330°)=√3/2 と求めることができます。
まとめるとどうなる?
とっていったポイントをまとめてみましょう。
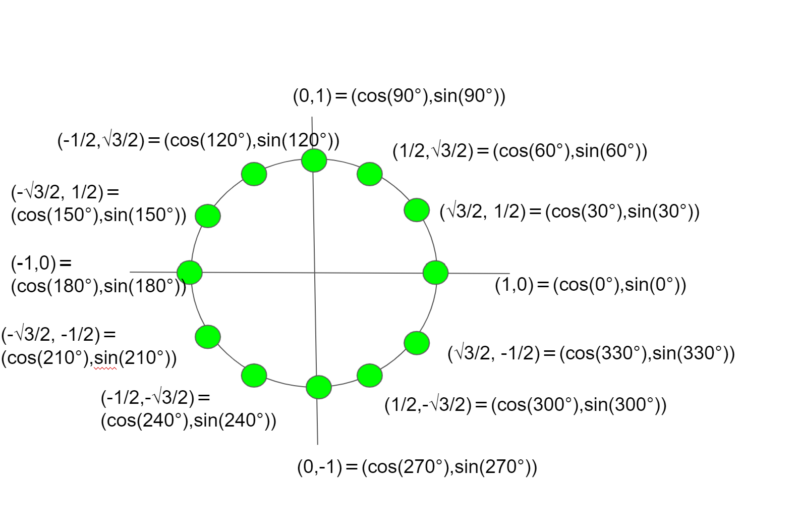
このx座標を0°から330°分を拾っていけば、コサインの値が出てきます。
数値的にわかりにくいのは、√3かもしれません。覚え方があって”ひとなみにおごれや”と覚えます。√3=1.7320508ですね。



コメント