コサイン、サインって覚えにくですよね。たとえば、コサインを参考書で見てみると、このような図がかいてありますよ。(三角形は直角三角形)
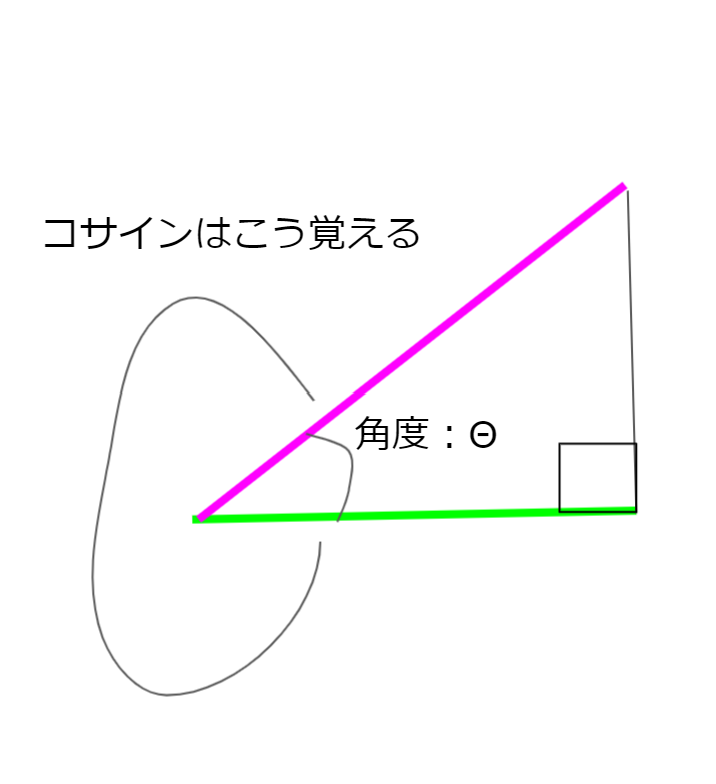
コサインのこう覚える、という線がコサイン(cos)の c に見える、と言いたいみたいです。cosの定義をもう一度見ておきましょう。cosは、直角三角形があったときに、角度Θのcosの値は、
cos(Θ)=緑の線長さ/紫の線の長さ
になります。例えば、紫の線の長さが5、緑の線の長さが4だとすると、
cos(Θ)=4/5
になります。
ところで、Θが30°とか60°のときはいいのですが、90°とか180°とかになると、どのようにcosを計算すればいいのでしょうか?
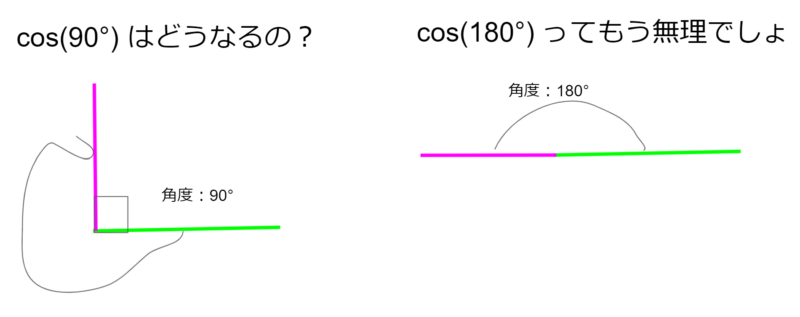
180°をみて絶望を感じた方のために、cosを再度定義してみます。ところで、単位円をご存じでしょうか。単位円は半径が1の円です。
ここで円周上にポイントをとって、x座標をx、y座標をyと置いてみましょう。紫が半径、緑の長さがx座標になっています。
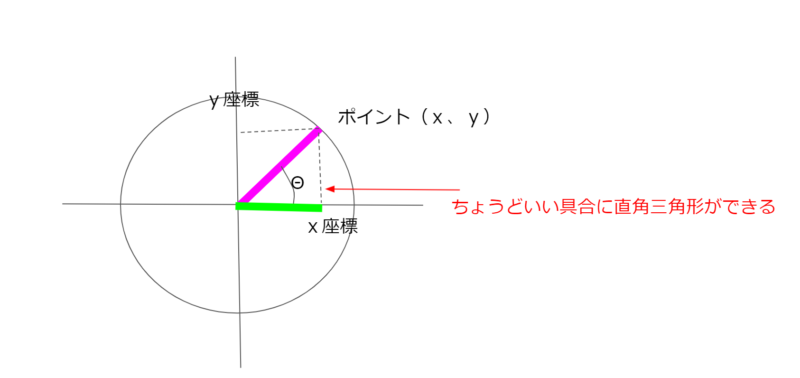
ちょうどいい具合に直角三角形ができています。これでcos(Θ)を計算してみると、
cos(Θ)=緑の長さ/紫の長さ
でしたので、
cos(Θ)=緑の長さ/紫の長さ=x座標/単位円の半径=x/1=x
となり、x座標の値がそのままcos(Θ)の値になります。そうすると、さっきのcos(90°)とかcos(180°)を計算することができます。ではcos(90°)がいくらになるか見てみましょう。下の図で、正のx軸からはかって90°は紫の点になります。ここのx座標は0なので、
cos(90°)=0
になります。
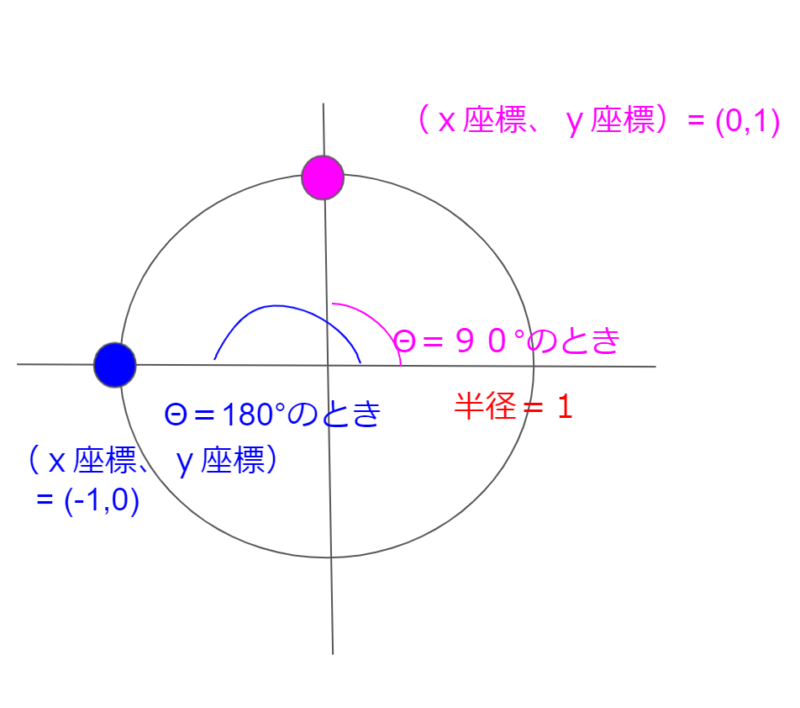
同様に、正のx軸からはかって180°は青のポイントになります。ここのx座標はー1ですので、
cos(180°)=-1
になります。
同様にサインも見てみましょう。まずはサイン(sin) の定義から。下のような三角形を考えましょう。すでに、紫色の線の長さは簡単のため1としてあります。
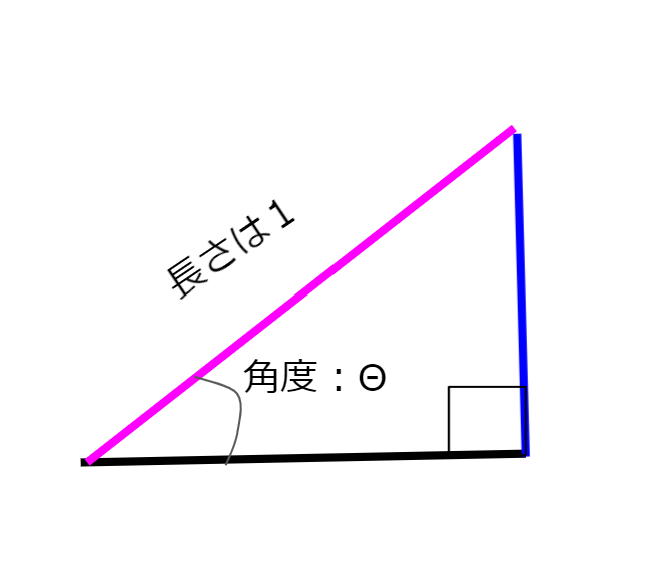
で、角度Θのサインの値は、
sin(Θ)=青線の長さ/紫線の長さ=青線の長さ/1=青線の長さ
になります。もう一度単位円を思い出しましょう。

図の中で青色の長さ、というとy座標になっています。ということは、
sin(Θ)=y座標
ということになります。
ということで、
ポイント(x,y)=(cos(Θ),sin(Θ))
となることがわかりました。ここで公式が1つあることに気がつきます。単位円の中の色のついた三角形は直角三角形なので、ピタゴラスの定理が成り立ちます。
(x座標)2+(y座標)2=(単位円の半径)2
ここで、x座標=cos(Θ)、y座標=sin(Θ)、単位円の半径=1を思い出すと、
[cos(Θ)]2+[sin(Θ)]2=1
が成り立ちます。
【弧度法について】
弧度法について触れておきましょう。角度は通常 °(度)なのですが、rad(ラジアン)という単位を導入します。定義はいろいろあるのですが、ここでは
180°=π(パイ)(rad)
と定義しましょう。πは円周率ですから、180°は約3.14(rad)ということになります。
角度は度でいいんじゃね、と思う方もおられるかもしれません。ラジアンという単位を導入するからには、何か便利になっておるはずです。例えばですが、下の図を見てみましょう。半径rの円から60°分を切り取った扇型です。
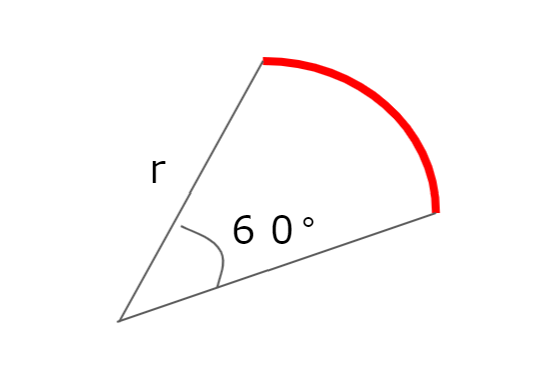
赤線の長さはいくら?と聞かれると、半径rの円の円周は2πr なので、60°分はその60/360をかければいいので、
赤弧の長さ=2πr × 60/360=πr/3
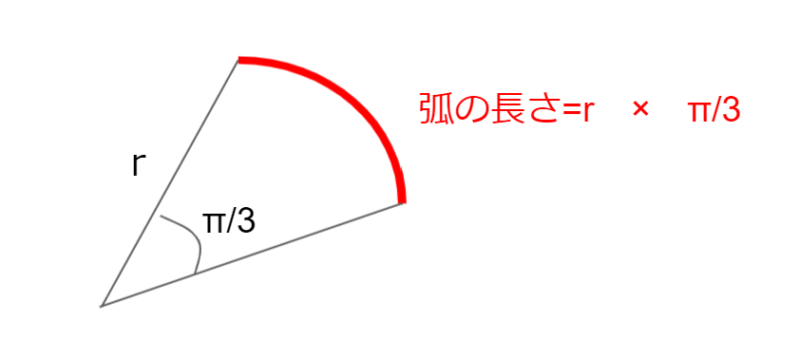
になります。ところで、60°はradに直すといくらかというと、
180° ーーー π (rad) だから、両辺を3で割って、
60° ーーー π/3 (rad)になります。
この扇型の角度 π/3 (rad) に半径r をかけた πr/3 が赤弧の長さになります。なので、弧度法はちょっと便利だったりします。
なぜここで弧度法を学んだかというと、pythonで三角関数を計算するときは、角度がradになっているので、知らない方向けにやってみました。



コメント