乱数を用いて面積を求めてみよう
面積を求める際に、いつも細かい短冊に区切って面積を求めていたのですが、今回は乱数を使って、円の面積を求めてみましょう。
乱数とは
例えば[0,1]間の乱数とは、[0,1]間に均等に散らばる数値に集まり、ということになります。pythonで乱数の書き方をみてみましょう。
import random
print(str(random.random()))
【プログラムを見てみよう】
乱数を使う場合は、import random を使います。
random.random() と書くことで、[0,1]の間にある乱数を1つ発生させます。print() の中に書くことで、打ち出しています。
0.8188791278107004
が出てきました。
では次に乱数を1000個発生させて、[0,1]の間に均等に数字が発生しているのか調べてみましょう。
import random kazu=[0]*10 #10個の要素を持つ配列を確認 print(str(kazu)) for i in range(0,1000,1): a=random.random() if a>=0 and a<0.1: kazu[0]=kazu[0]+1 elif a>=0.1 and a<0.2: kazu[1]=kazu[1]+1 elif a>=0.2 and a<0.3: kazu[2]=kazu[2]+1 elif a>=0.3 and a<0.4: kazu[3]=kazu[3]+1 elif a>=0.4 and a<0.5: kazu[4]=kazu[4]+1 elif a>=0.5 and a<0.6: kazu[5]=kazu[5]+1 elif a>=0.6 and a<0.7: kazu[6]=kazu[6]+1 elif a>=0.7 and a<0.8: kazu[7]=kazu[7]+1 elif a>=0.8 and a<0.9: kazu[8]=kazu[8]+1 elif a>=0.9 and a<1: kazu[9]=kazu[9]+1 print(str(kazu))
【プログラムを見てみよう】
kazu=[0]*10 で、中身が0で、要素の数が10個の配列を作ります。これでprintで打ち出してみると、
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
になっています。見方は、
- kazu[0]=0
- kazu[1]=0
- kazu[2]=0
- …
- kazu[9]=0
ということになります。
if a>=0 and a<0.1:
kazu[0]=kazu[0]+1
は、発生した乱数が、0以上0.1未満のとき、kazu[0]の値を1つプラスします。つまり、数をカウントさせています。なので、ここのif文は、[0,1]の間を0.1間隔で区切って、各間隔ごとに乱数がいくつあるかカウントしています。
結果を見てみましょう。
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[109, 99, 93, 100, 95, 108, 101, 117, 91, 87]
要素を見ていると、大体100個ぐらい入っています。[0,1]の中で0.1間隔で区切ったときに、大体均等に散らばっていることがわかります。
モンテカルロ法について
では乱数を使って、円の面積を求めてみましょう。正方形の中に乱数をプロットすることを考えてみましょう。
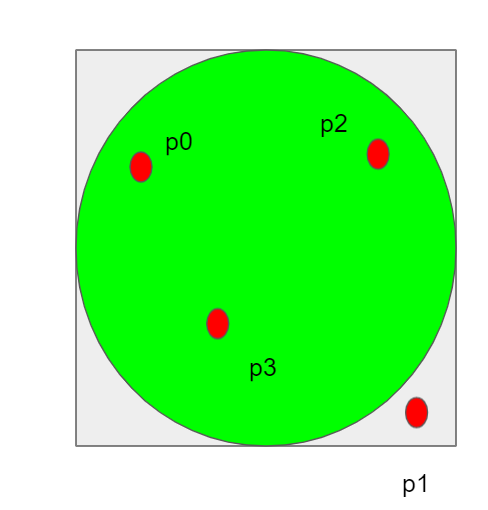
図のように正方形の中に乱数をプロットしていきます。乱数ですので、正方形の中に均等にプロットされていきます。乱数ですので、どこかに偏る、ということはありません。
正方形の中にプロットする際に、円の中にプロットされるポイントの数を数えると、以下が近似的に成立することが予想できます。
正方形の面積:円の面積=正方形の中のプロット数:円の中のプロット数
半径1の円の式は、x2+y2=1 であることは以前確認しました。円の内部は、x2+y2<1、円の外部はx2+y2>1 が成り立ちます。
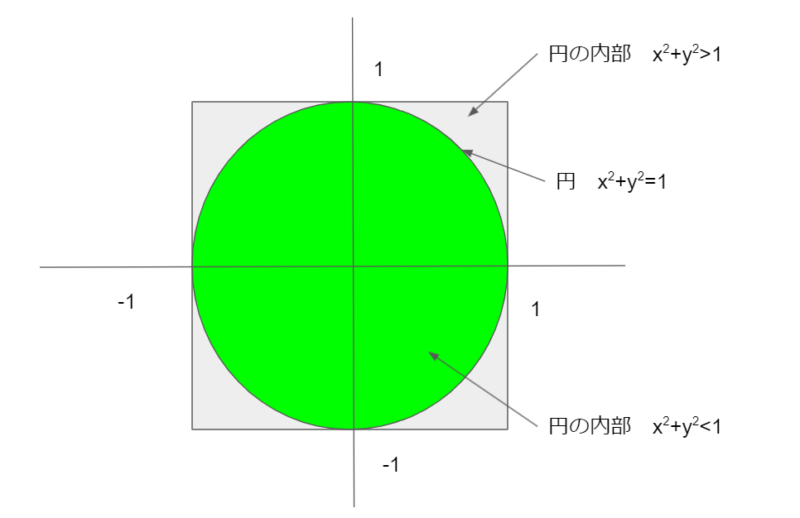
例えば、(0.5,0.5)が円の内部が外部かというと、
x2+y2=0.52+0.52=0.25+0.25=0.5<1
なので、(0.5,0.5)は円の内部にあります。
pythonで円の面積を求めてみよう
では、半径1の円の面積を求めてみましょう。半径1の円なので、正方形の面積は2×2=4になります。なので、
正方形の面積:円の面積=正方形の中のプロット数:円の中のプロット数
なので、
4:円の面積=正方形の中のプロット数:円の中のプロット数
から
(円の面積)×(正方形の中のプロット数)=4×(円の中のプロット数)
なので、
円の面積=4×(円の中のプロット数)/ (正方形の中のプロット数)
になります。以上を踏まえて、pythonでプログラムを組んでみましょう。
import random total=10000 en=0 for i in range(0,total,1): a=random.uniform(-1,1) b=random.uniform(-1,1) if a*a+b*b<1: en=en+1 en_menseki=4.0*en/total print(str(en_menseki))
【プログラムを見てみよう】
totalで、いくつ点を打つか決めています。
random.uniform(-1,1) で、(-1,1)の間の乱数を発生させます。a,bの2個発生させて(a,b)という点を正方形の中にプロットしていると想定しています。
この(a,b)が円の内部にあれば、enにカウントしていきます。
最後に en_menseki で円の面積を求めています。
結果は
3.1696
でした。半径1の円の面積は、πr2=π12=3.14
ですので、結構近い値が出ています。
さらに学習を進めたい方に
python初心者の方は
Pythonの絵本 Pythonを楽しく学ぶ9つの扉 [ 株式会社アンク ]
他の言語もかじった方は



コメント