面積を表す関数を微分するとどうなるでしょうか?
面積を表す関数を下の図のように定義してみます。
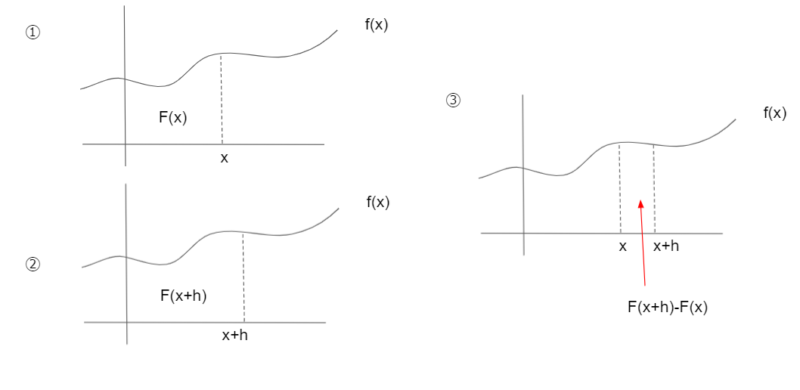
【①の場合】
曲線f(x)があるとします。曲線と、x軸、y軸、xの点線部分で囲まれる面積をF(x)としましょう。
【②の場合】
曲線と、x軸、y軸、x+hの点線部分で囲まれる面積をF(x+h)としましょう。
【③の場合】
曲線とx軸、x,x+hの点線で囲まれた面積は、F(x+h)-F(x)になります。
ところで、この③の短冊の面積は、hの値が小さければ、以下のように近似することができます。
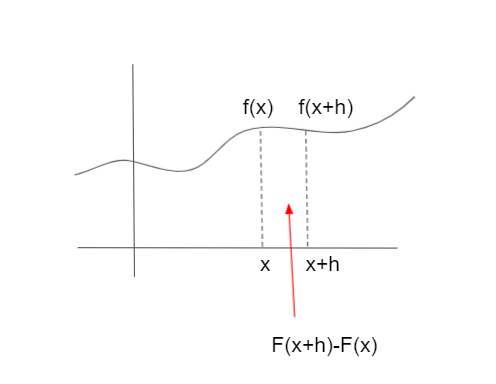
hが十分小さいときは、f(x+h)=f(x)とみなせます。なので、赤矢印で示した面積は、f(x)を使うと、
f(x)×h
とも書けます。
なので、
短冊の面積=f(x)×h=F(x+h)-F(x) (hが十分小さい場合です)
と書けます。両辺hで割れば、
f(x)=( F(x+h)-F(x) )/h (hが十分小さい場合です)
ここで、オヤッ、とおもいますよね。
( F(x+h)-F(x) )/h (hが十分小さい場合です)
はまさに微分の定義そのものです。なので、
f(x)=F'(x)
という関係式が成り立ちます。
f(x)=x2のとき、F(x)は?
g(x)=xnのとき、g(x)の微分であるg'(x)は
g'(x)=nxn-1
であることは過去確認しました。注意すべき点は、微分するとxの肩の次数が一つ減る、ということです。
さて、f(x)=x2のときf(x)=F'(x)を満たすF(x)を求めてみましょう。
F(x)を微分してx2になればいい。微分すると次数が一つ減るので、F(x)はx3に違いない。
F(x)=x3 と思って微分してみよう。
F'(x)=3x2 になってしまって、3が余分ですね。なので、
F(x)=x3 /3 としてみて微分すると、
F'(x)=3x2 /3=x2
になりました。これで晴れて、
(x3 /3)’=x2
が確認できました。
積分を定義しよう
微分の逆の計算をすることを、積分といいます。
- x3 /3 から x2 を導くのが微分
- x2 から x3 /3 を導くのが積分
となります。
積分を利用すると、面積の理論値を求めるのは簡単
f(x)=x2のとき、下の図の面積を求めてみましょう。
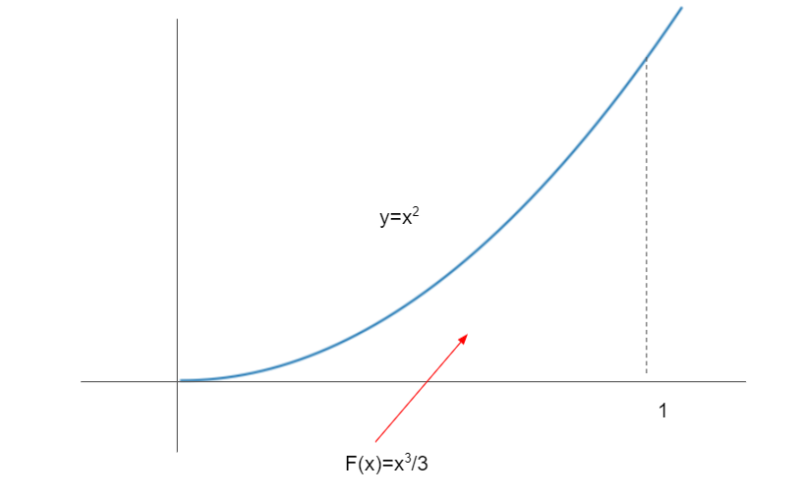
以前、pythonを用いて実験値を求めてみました。大体1/3 でした。
理論値を計算してみると、
f(x)=x2
積分するとF(x)=x3 /3 (定数項は無視しています)
x=1のときの面積なので、F(1)=1/3
となります。理論値と実験値が一致しました。
f(x)=x4のとき面積は?
x=1のときの面積を求めてみると、
F(x)=x5/5
なので、
F(1)=1/5です。これが理論値です。では、実験値はどうなるでしょうか。pythonで確認してみましょう。
import math pi=math.pi kaisu=100 h=1/kaisu x=0 menseki=0 for i in range(0,kaisu,1): menseki=menseki+ math.pow(x,4)*h x=x+h print(str(menseki))
【プログラムを見てみよう】
[0,1]の間隔を100分割して面積を求めています。100分割する値が kaisu 、短冊の幅が h になります。
math.pow(x,4)*h が短冊の面積ですので、for文の中で、幅の小さい短冊を次々足しこんでいって、mensekiにため込んでいきます。結果を見てみましょう。
0.19503333300000053
理論値(1/5)に近い値が出ました。hの幅をどんどん0に近づければ、1/5に近づいていきます。
さらに学習したい方に
pythonの初心者マークの方は
Pythonの絵本 Pythonを楽しく学ぶ9つの扉 [ 株式会社アンク ]
他の言語もかじりました系の方は



コメント