コサインを微分する?
コサインを微分すると、-sinになります。
(cos(Θ))’ = -sin(Θ)
実はこの辺りから解説しないといけないのですが、事前準備がいろいろ必要なので、もう少し進んでからにします。(オイラーの定理をご存じの方はすぐにできます。)
ちなみにオイラーの定理とは、
eiΘ=cos(Θ)+i sin(Θ) (e:自然対数 i:虚数)
です。何気にすごい式なんです。実用的にもよく使います。
ここでは、実験的にコサインを微分したら、ーサインが出ることを見ていきましょう。
pythonでコサインの微分を実験
ではプログラムを見てみましょう。
import math import matplotlib.pyplot as plt pi=math.pi h=0.00001 bibun=[] for i in range(0,360,1): a=i*pi/180 bibun.append( (math.cos(a+h)-math.cos(a))/h) plt.plot(bibun) plt.show()
【プログラムを見てみよう】
for 文の中で、0°から359°までの微分の近似値を計算しています。(1周分です。)for 文の中の i は°(度)で、この値をradに変換します。そして、h=0.00001 として、2点間を結ぶ線を求めます。hが小さければ小さいほど、iのポイントでの接線に近くなります。
結果を見てみましょう。
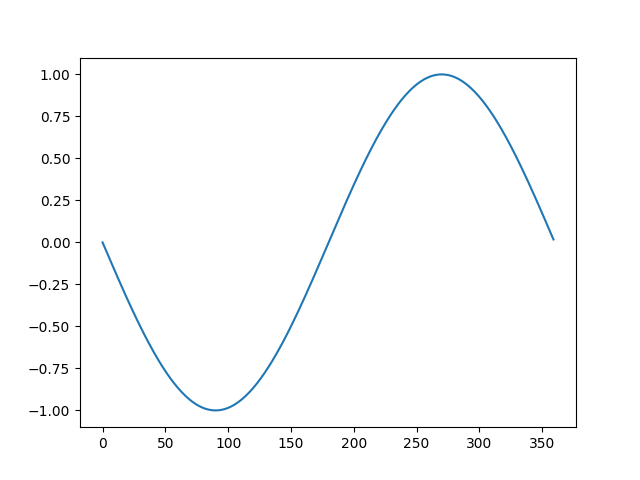
サインのグラフの上下をさかさまにしたグラフ、つまり -sin のグラフが描けました。
サインの微分も実験してみよう
同じ方法でサインの微分もみることができます。ちなみに、
(cos(Θ))’=sin(Θ)
です。ではプログラムを見てみます。
import math import matplotlib.pyplot as plt pi=math.pi h=0.00001 bibun=[] for i in range(0,360,1): a=i*pi/180 bibun.append( (math.sin(a+h)-math.sin(a))/h) plt.plot(bibun)plt.show()
【プログラムを見てみよう】
先ほどの、math.cos から math.sin に変わっただけです。
では結果を見てみましょう。

コサインのグラフを描くことができました。
オイラーについて
オイラーはスイスの数学者で、ガウスと並んで、2大数学者と言われています。(確かそう)歳をとってから両目を失明したらしいのですが、それでも数学の研究をして、生涯で多数の論文を残しています。オイラーの業績は多すぎて、まだ全体を完全には把握できていないといわれています。
さらに学習をされる方は
python初心者の方はこちら
Pythonの絵本 Pythonを楽しく学ぶ9つの扉 [ 株式会社アンク ]
他の言語をかじった系の方はこちら
オイラーの面白い読み物については



コメント