曲線の接線を求めてみよう
y=x2のグラフを考えてみましょう。せっかくなので、pythonで確認してみましょう。
import math import matplotlib.pyplot as plt x=[] atai=[] for i in range(-9,10,1): x.append(i) atai.append(i*i) plt.plot(x,atai) plt.show()
x2は、atai.append(i*i)で計算しています。
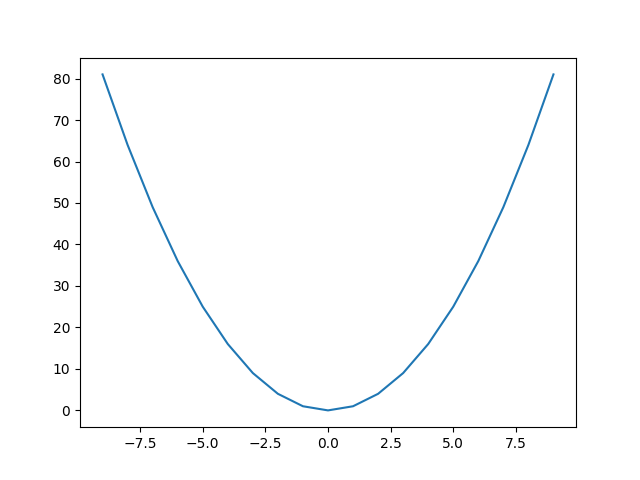
この線は放物線といいます。物を投げると、引力の関係でこのような形で飛ぶ、ということです。(ものを投げる場合は、このグラフの上下逆さにしたものになります)
次に、放物線の接線を考えてみましょう。接線とは、放物線と接する線になります。
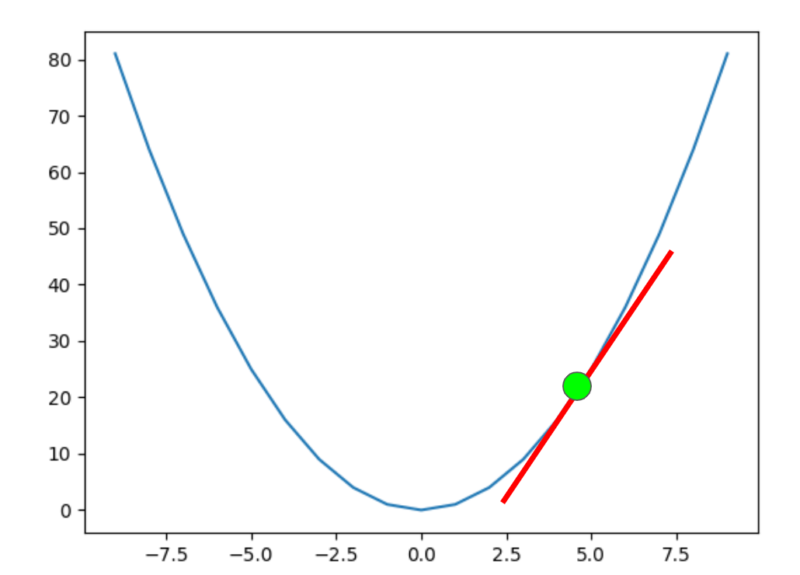
緑の点の接線は、赤線になります。
この接線はどのように求めればいいでしょうか。
x=5での接線を求めてみることにしましょう。もう一つ勝手にx=7.5のところにもポイントをとってみましょう。
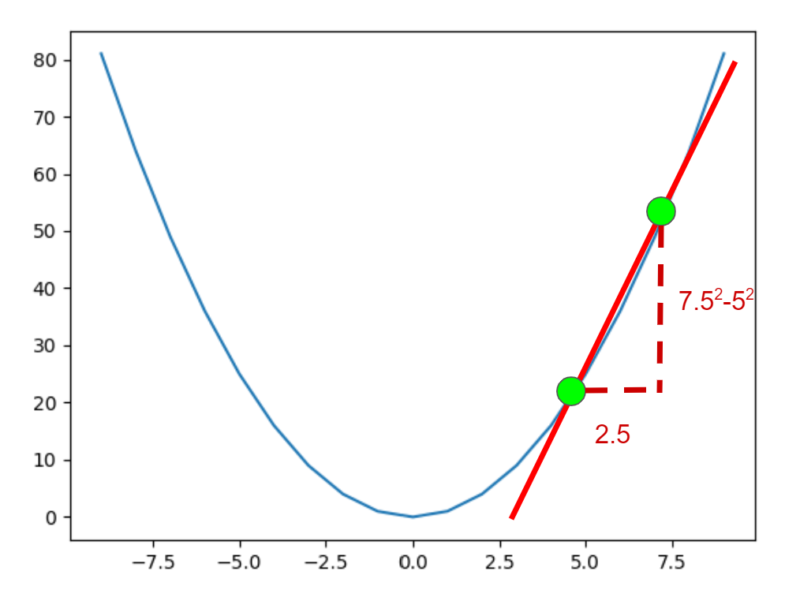
緑のポイントのy座標は、y=x2を思い出すと、52と7.52になります。緑のポイントを線で結ぶと何となく接線のような線が引けます。でも接線とはわずかに違います。
とはいえ、ここで引き下がりません。このx=7.5のところにポイントをとりましたが、x=5のポイントにどんどん近づけていけば、2点を結ぶ直線は、x=5での接線にどんどん近くなります。図に書き直しましょう。
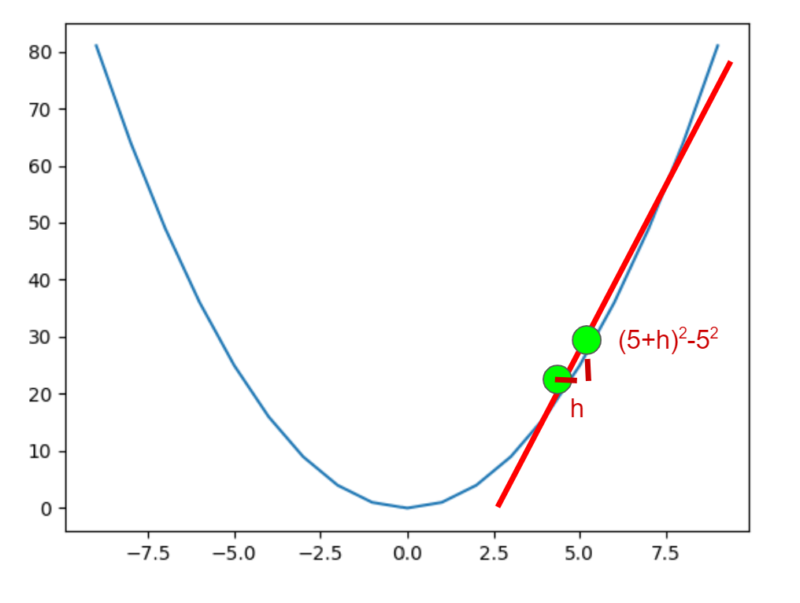
x=5と、そこからh離れた点をむすんでみます。x=5のポイントの座標は(5,52)、x=5+hのポイントの座標は(5+h、(5+h)2)ですので、この直線の傾き(yの増加量/xの増加量)を計算してみます。
yの増加量/xの増加量={(5+h)2 - 52}/{ (5+h) – 5}
これを計算してみましょう。
yの増加量=(5+h)2 - 52 =25+10h+h2 – 25 =h2+10h
xの増加量=5+h -5=h
なので、
yの増加量/xの増加量=(h2+10h)/ h =h+10
になります。ここで、hを0に近づければ、2つのポイントを結ぶ線は、x=5での接線に限りなく近くなります。yの増加量/xの増加量の結果 h+10のhを0に近づければ、接線の傾きは10に限りなく近づいていきます。
pythonで確認してみよう
x=5での接線を確認してみましょう。
h=1 for i in range(0,5,1): atai=( ((5+h)*(5+h)-5*5)/(5+h-5) ) h=h*0.1 print(str(atai))
【プログラムの注意点】
hはfor の中で、h=h*0.1 としていますので、forの計算が繰り返すたびに、0.1倍になっていきます。(どんどん間隔が狭くなる。)結果を見てみましょう。
11.0
10.100000000000016
10.009999999999977
10.000999999999252
10.000100000008274
どんどん10に近づいていきます。
lim を確認しよう
先ほど、hを0に近づける、というお話をしましたが、この作業を表す記号があります。
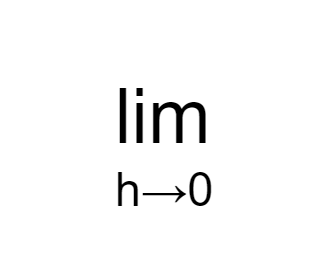
limはリミットと読みます。この記号の意味は、hを限りなく0に近づける、という意味になります。ピッタリ0にはなりません。ここが、limの意味のポイントです。ですので、先ほどの h+10 のhを0に限りなく近づける、というのは、

になります。
さらに学習したい方は
python始めます系の方は
Pythonの絵本 Pythonを楽しく学ぶ9つの扉 [ 株式会社アンク ]
他の言語をかじった系の方は



コメント