円の式の表現はどうなる?
半径rの円の面積は、πr2です。これを公式を知らないと仮定して、プログラムで求めてみましょう。ここでは簡単にr=1としましょう。この場合、円の面積はπになります。
まず円は式ではどのように書けるかを考えてみましょう。
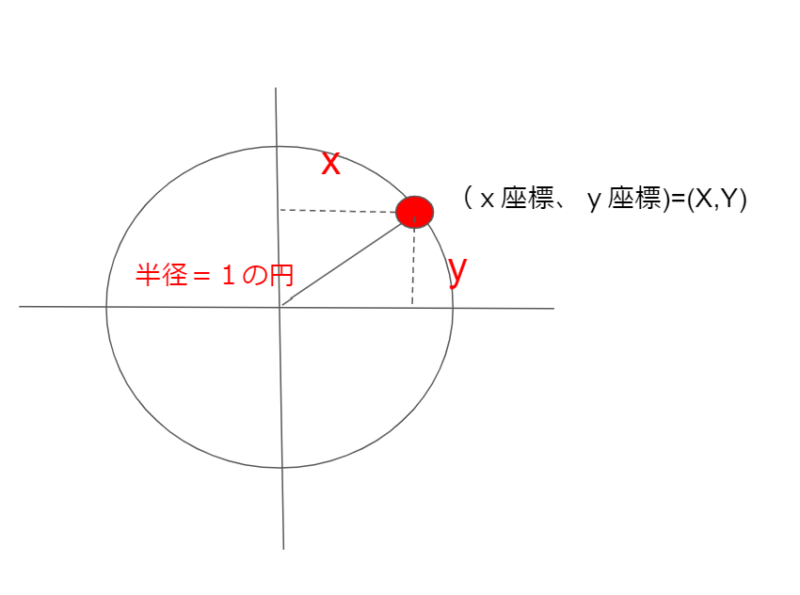
半径1の円上に(x、y)のポイントを取ると、ピタゴラスの定理から、
x2+y2=12
が成立します。これは(x、y)が円周上のどこにあっても成立します。
面積を求めるには?
この式をy=の形に直します。
y2=1-x2
なので、
y=±√(1-x2)
になります。yに±が付いていますが、
- (プラスのとき)y=√(1-x2) は、円の上半分、
- (マイナスのとき) y=-√(1-x2) は円の下半分
を表しています。
円の面積を求めるのに、以下の部分の面積を求めて4倍することにします。
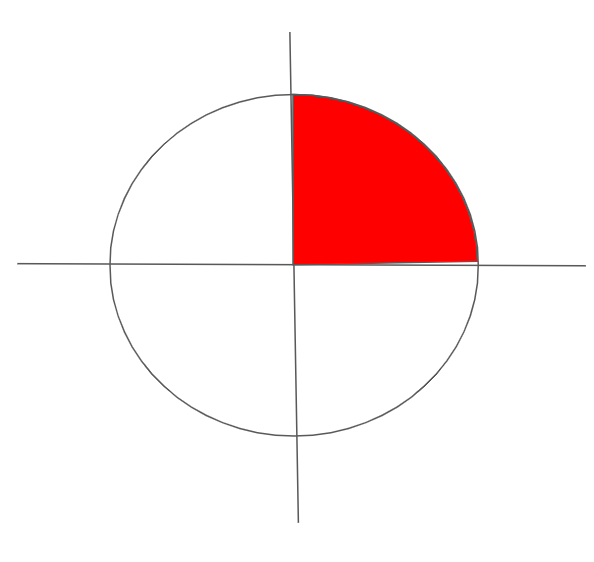
では、この赤い部分を例のごとく、長方形の短冊に分割して面積を求めてみましょう。
プログラムを確認しよう
今回のプログラムは、短冊の横の幅をいろいろ変えられるようにしてみましょう。
import math bunkatu=10000 haba=1/bunkatu menseki0=0 x=0 for i in range(0,bunkatu,1): menseki0=menseki0+math.sqrt(1-x*x)*haba x=x+haba print(str(menseki0*4)) menseki1=0 x=0 for i in range(0,bunkatu,1): x=x+haba if x>1: x=1 menseki1=menseki1+math.sqrt(1-x*x)*haba print(str(menseki1*4))
このプログラムは、bunkatuに入れる数値で、短冊の幅(1/bunkatu)を調整できるようにしました。
真の面積よりちょっと大きい面積をmenseki0、ちょっと小さい面積をmenseki1に入れています。
プログラムを見てみよう
まず短冊の面積を確認します。ルートはプログラムでは、
math.sqrt()
xの2乗は
x*x
と書きますので、√(1-x2)は、
math.sqrt(1-x*x)
ですので、これに短冊の幅を掛けた、
math.sqrt(1-x*x)*haba
が短冊1つの面積になります。
最後に面積を4倍して、円の面積を求めます。
ちょっと気になるのが、if文です。ここで何をしているかといいますと、プログラムの特徴なのですが、小数はプログラムでは正確には表現できないことに関係があります。機会があれば取り上げようかと思いますが、プログラムの中では、数値は2進数で表現されているのが原因です。
理論ではプログラム内のxのmaxの値は1なのですが、プログラム内では1を微妙に超えます。その場合、
√(1-x2)
のルートの中が負の数になり、全体として虚数になってしまいます。ですので、if文を書くことで、この問題を回避しています。
結果を見てみよう
計算結果は、
3.1417914776115916(真の面積よりちょっと大きい)
3.1413914777848557(真の面積よりちょっと小さい)
となります。真の面積はこの間にあるわけですから、共通した部分をとれば、
3.141
という値が求まります。プログラムが合っていれば、円周率に近い値が出てきます。



コメント