コサインのグラフを復習しよう
最初に、y(x)=cos(x) (x:0-360°)のグラフをpyhtonを使って描いてみましょう。これは復習になります。横軸は時間ではなくて、°になってます。
import math import matplotlib.pyplot as plt pi=math.pi x=0 y=[] while x<360: sita=x*pi/180 y.append( math.cos(sita) ) x=x+1 plt.plot(y) plt.show()
【プログラム復習】
xが0°から360°までを描くのですが、°からラジアンに変換しないといけません。ラジアンを思い出すと、π(ラジアン)=180°なので、x°はx×π/180(ラジアン)になります。
【結果】
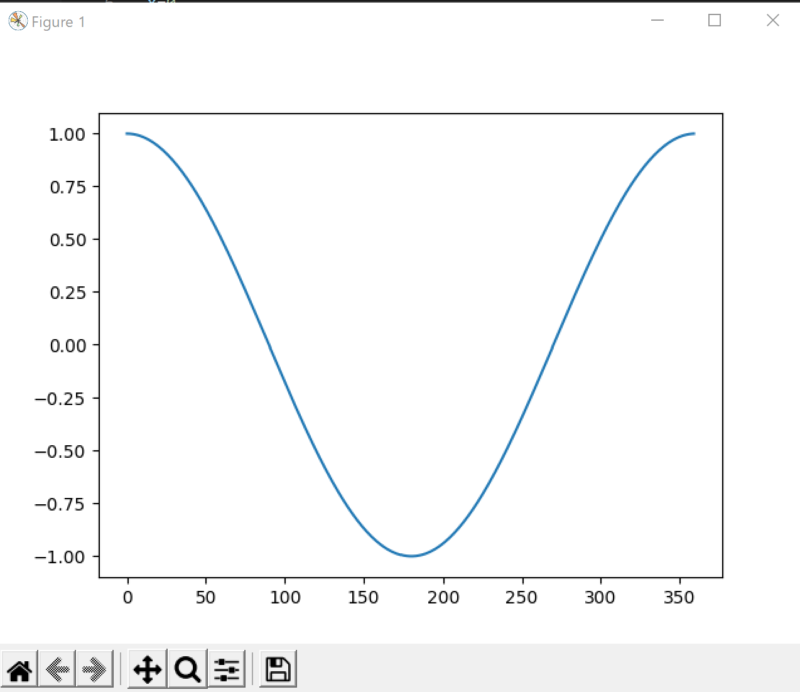
になります。
0°から90°の間の面積を求めてみよう
cos(90°)=0でしたので、[0°,90°]の範囲は、以下のようになります。
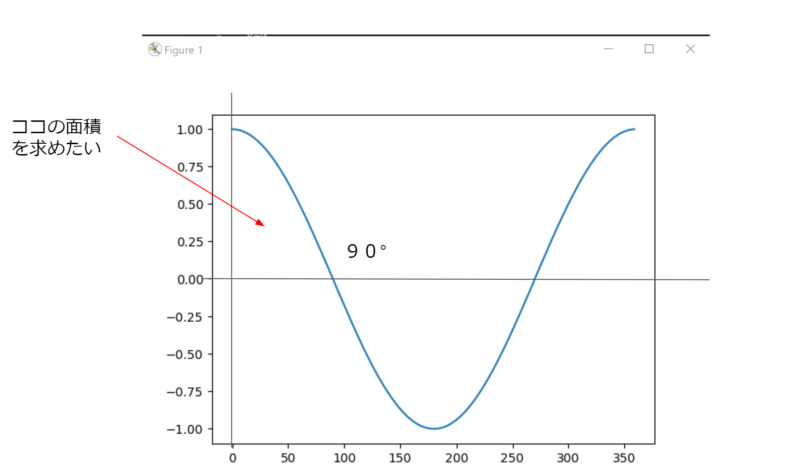
今回は、矢印の部分(コサイン波とx軸、y軸に囲まれた部分)の面積を求めてみましょう。
前回と同じように短冊に分割して足し算していきます。まずは、0°以上90°未満の範囲で、短冊の横幅は、1(ラジアン=π/180)としています。
import math menseki=0 pi=math.pi kankaku=pi/180 for i in range(0,90,1): sita=i*pi/180 menseki=menseki+math.cos(sita)*kankaku print(str(menseki))
結果は、1.008位になります。
次に、0°より大きく90°以下の範囲で面積を計算してみましょう。
import math menseki=0 pi=math.pi kankaku=pi/180 for i in range(1,91,1): sita=i*pi/180 menseki=menseki+math.cos(sita)*kankaku print(str(menseki))
計算結果は、0.9912でした。
真の面積は、
0.9912(下限)<真の面積<1.008(上限)
の範囲になります。ちなみに、真の値は1になります。短冊の幅を1ラジアンにしていますが、もっと小さくとれば、上限、下限とも1に近づきます。
(短冊の横幅をもっと小さくとれば) 1に近づく(下限)<真の面積<1に近づく(上限)
pythonのチェックポイント
for 文の中で、i in range(0,90,1) と range(1,91,1) の場合で、iはいくつからいくつまで、値が入るか確認してみましょう。
90は数値が大きいので、5ぐらいで考えてみましょう。
for i in range(0,5,1)
とすると以下のように解釈します。
for i(iの値は) in range(0(0から),5(5未満で),1(1間隔で))
なのでiには、0,1,2,3,4(5はいかない)になります。なので、
range(0(0から),90(90未満で),1(1間隔で))
range(1(1から),91(91未満で),1(1間隔で))
になります。
確認する場合は、次のように確認してみるといいでしょう。
for i in range(1,91,1): print(str(i))



コメント