コサイン波を足すのは簡単、では分解は?
例えば周波数1,3,5のコサイン波を足し合わせると、
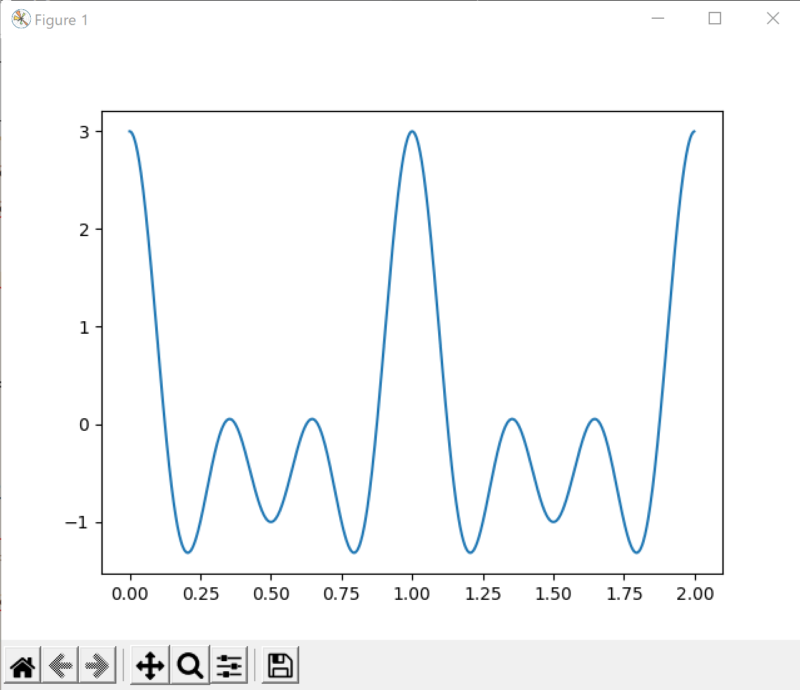
足し合わせは、足せばいいんですけど、では逆に分解できますか?ということを考えてみます。分解とはつまり、このグラフの波形から、周波数1,3,5の波がある、ということをつきとめることができますか?、ということになります。
考える前に準備をしましょう
周波数が同じコサイン波を掛けて足し合わせる
周波数が1Hzのコサイン波を掛け合わせて、結果を足し合わせてみます。言葉で言ってもよく意味が通らなので、イメージ図を見てみましょう。
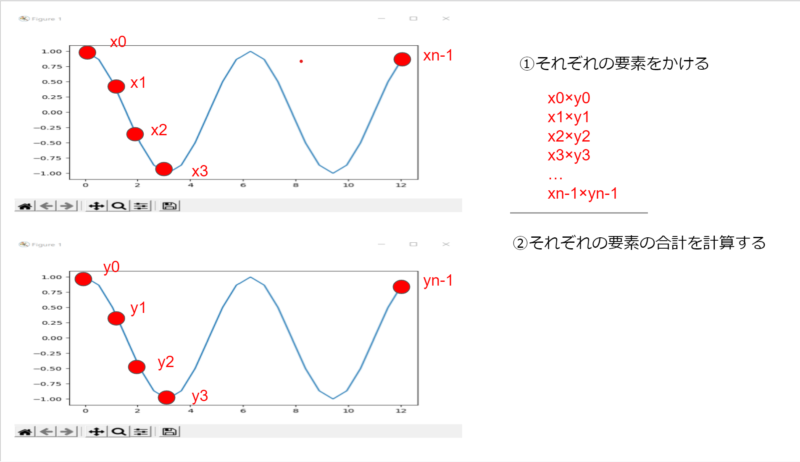
図にあるコサイン波は両方周波数1のコサイン波なのですが、2つは違う波形ととらえて、各ポイントの掛け算を計算します。
x0×y0、x1×y1、x2×y2、・・・xn×yn、を計算します。
これらをすべて足し合わせます。(ここまでイメージ図)この結果を点の個数nで割って、この値を観察します。プログラムを見てみましょう。
import math pi=math.pi n=0 t=0 kaisu=0 while t<2: sita=2*pi*t a=math.cos(sita) n=n+a*a kaisu=kaisu+1 t=t+0.002 n=n/kaisu print(str(n))
【コードを見てみよう】
プログラムは図の点(x0,x1など)の値をaで表しています。sitaの値が t 毎に変化するので、sitaの値もwhileの中の計算を繰り返すごとに変わっていきます。
n=n+a*a
で、a*aの値を次々足しこんでいきます。
kaisu=kaisu+1
は何回while文の中身の計算をしたか、をカウントしています。100回繰り返せば、kaisu=100になります。
最後に計算が終われば、n=n/kaisu で足し合わせた結果を、ループの回数で割ります。
実行すると、
0.5000000000000004
となりました。
周波数の違うコサイン波を掛けわせるとどうなる?
では次に、周波数1のコサイン波と周波数2のコサイン波を掛け合わせるとどうなるか、プログラムで見てみましょう。
import math pi=math.pi n=0 t=0 kaisu=0 while t<2: sita=2*pi*t a=math.cos(sita) b=math.cos(2*sita) n=n+a*b kaisu=kaisu+1 t=t+0.002 n=n/kaisu print(str(n))
【コードを見てみます】
ほとんど一緒なのですが、bで周波数2のコサイン波を生成し、n=n+a*b として和をとっています。
結果を見てみましょう。
7.334133300673784e-16
e-16は10-16ということなので、0に非常に近い値なので、0とみなしていいです。
もっひとつおまけで、 bのところを b=math.cos(3*sita) に変えるとどうなるでしょうか。
8.525402606096577e-16
という結果が得られます。0とみなしていい数値が出てきます。
足し合わせの波形で同じことをしてみます
以上を踏まえて、同じことをコサインの足し合わせのグラフでやってみます。周波数1,3,5Hzのコサイン波の足し合わせ波形を作り、周波数5Hzまでの範囲で、書く周波数の有り無しを見てみましょう。プログラムはもっと簡単にかけるのですが、読者さんはプログラム習い始めの方を想定していますので、効率よりも簡単さ重視で書いています。
import math
pi=math.pi
t=0
kaisu=0
cos_1=0
cos_2=0
cos_3=0
cos_4=0
cos_5=0
while t<2:
sita=2*pi*t
a=math.cos(sita)+math.cos(3*sita)+math.cos(5*sita)
cos_1=cos_1+a*math.cos(sita)
cos_2=cos_2+a*math.cos(2*sita)
cos_3=cos_3+a*math.cos(3*sita)
cos_4=cos_4+a*math.cos(4*sita)
cos_5=cos_5+a*math.cos(5*sita)
kaisu=kaisu+1
t=t+0.002
cos_1=cos_1/kaisu
cos_2=cos_2/kaisu
cos_3=cos_3/kaisu
cos_4=cos_4/kaisu
cos_5=cos_5/kaisu
print('cos_1='+str(cos_1))
print('cos_2='+str(cos_2))
print('cos_3='+str(cos_3))
print('cos_4='+str(cos_4))
print('cos_5='+str(cos_5))【コードを見てみよう】
cos_1からcos_5に、重ね合わせた波形と、各周波数のコサイン波の和を取り込んでいきます。whileの中で計算できたら、whileで繰り返した数(kaisu)で割ります。結果をprintで打ち出します。
print(str(cos_1))
とすると、結果を見ると何の計算結果はわからないので、
print(‘cos_1=’+str(cos_1))
と書いておきます。これで、数値に前に、cos_1=を書くことができます。ただし+が必要になります。つまり、
print(‘cos_1=’str(cos_1)) (誤り構文)
これでは動きませんので注意しましょう。
結果を見てみましょう。
cos_1=0.5000000000000018
cos_2=2.191136161400209e-15
cos_3=0.5000000000000019
cos_4=2.283506717049022e-15
cos_5=0.5000000000000026
これを見ると、周波数1,3,5の成分はある、周波数2,4の成分はない、ということがわかります。
pyhtonプログラムのチェックポイント
回数をカウントしているkaisuは、以下のような形になっています。
kaisu=0
while t<2:
kaisu=kaisu+1この形で、whileの中が何回実行されたか確認できます。1回目のwhileが実行されると、どうなるかというと、
- まずkaisu=0である
- kaisu=kaisu+1 なので、これはkaisu←kaisu+1 と解釈する
- kaisu=0なので、kaisu←0+1なので、kaisuは1になる。
- 2回目にwhileが実行されると、kaisu=1なので、kaisu←1+1 でkaisu=2になる
以下同様です。n=n+a*aも同様の解釈で理解できると思います。



コメント