サインのグラフも書いてみる
前回コサインのグラフを書いてみました。今回は、コサインとサインのグラフを書いてみましょう。さっそく以下のコードを書いてみます。
import math import matplotlib.pyplot as plt pi=math.pi kakudo_rad=[] cos_atai=[] sin_atai=[] for kakudo in range(0,720,30): sita=kakudo*pi/180 kakudo_rad.append(sita) cos_atai.append(math.cos(sita)) sin_atai.append(math.sin(sita)) plt.plot(kakudo_rad,cos_atai) plt.plot(kakudo_rad,sin_atai) plt.show()
前回と違うところは、
sin_atai=[]
でサインの値を収納する空箱を作り、ここにfor文の中で、コサインと同じように、サインの値を取り込んでいきます。サインの値は
math.sin()
で計算してあります。ではさっそく実行してみましょう。
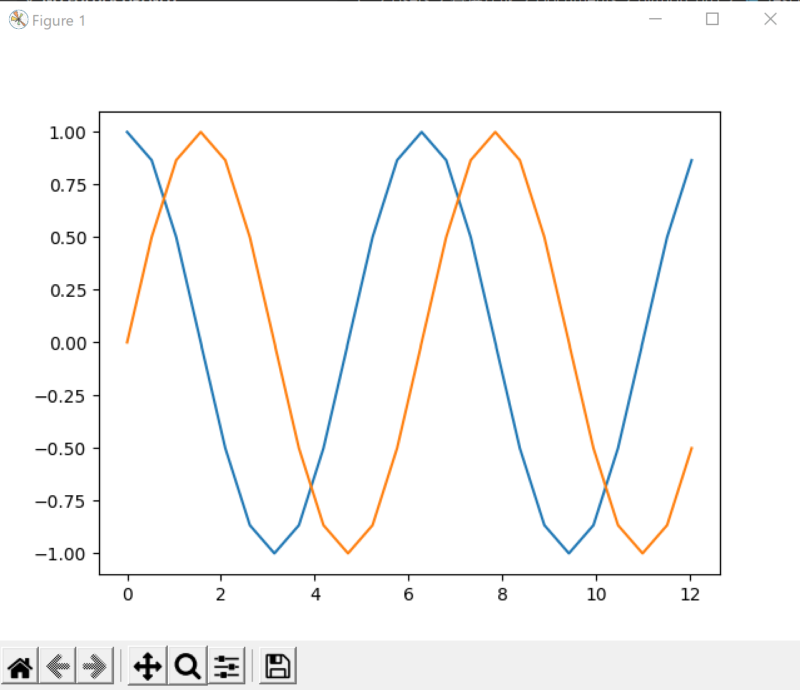
青色がコサイン、オレンジ色がサインです。ただこれだと一見してどれがどれだか判断しずらいですので、凡例をつけることにします。
まず、plt.plot()のところで、labelを追加します。
plt.plot(kakudo_rad,cos_atai,label=’cos’)
plt.plot(kakudo_rad,sin_atai,label=’sin’)
そして、plt.show()の前に、
plt.legend()
を追加します。再度、コードを見てみましょう。
import math import matplotlib.pyplot as plt pi=math.pi kakudo_rad=[] cos_atai=[] sin_atai[] for kakudo in range(0,720,30): sita=kakudo*pi/180 kakudo_rad.append(sita) cos_atai.append(math.cos(sita)) sin_atai.append(math.sin(sita)) plt.plot(kakudo_rad,cos_atai,label='cos') plt.plot(kakudo_rad,sin_atai,label='sin') plt.legend() plt.show()
実行してみます。
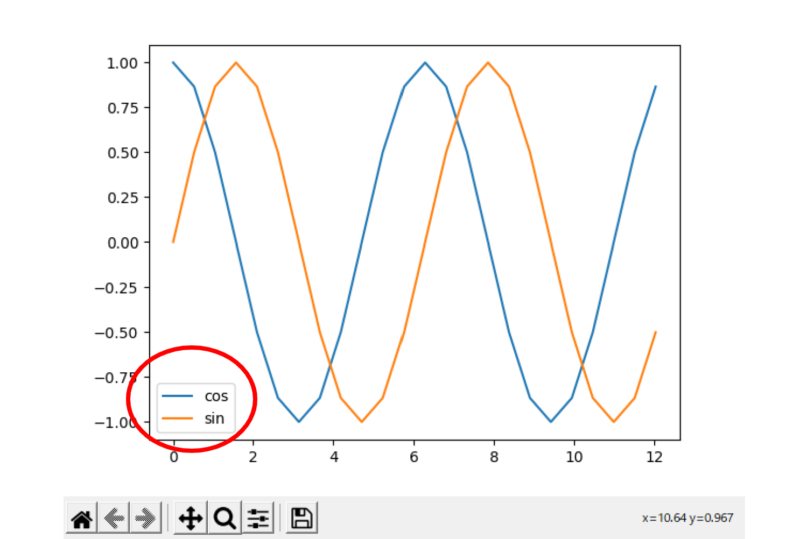
赤丸の凡例が追加され、その線がサインかコサインか、わかりやすくなりました。
もう少しきめ細かくグラフを書きたい
サインとコサインのグラフを見ていると、カクカクしてますよね。本当は、コサインやサインのグラフは滑らかになっています。先ほどのグラフは30°毎にコサイン、サインのポイントを取りグラフにしていますが、今度は5°毎にコサイン、サインのグラフを描いてみましょう。変更するのは、
for kakudo in range(0,720,30):
を
for kakudo in range(0,720,5):
に変更するだけです。
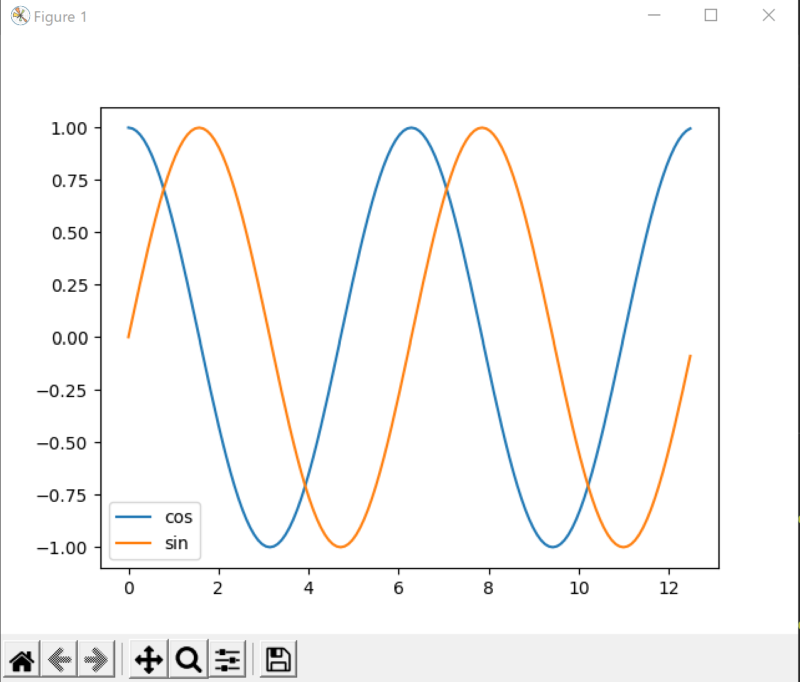
グラフが滑らかになりました。
周波数の話
周波数というのは、波が1秒間の中にいくつあるか?、を表しています。例えばコサインのグラフであれば、
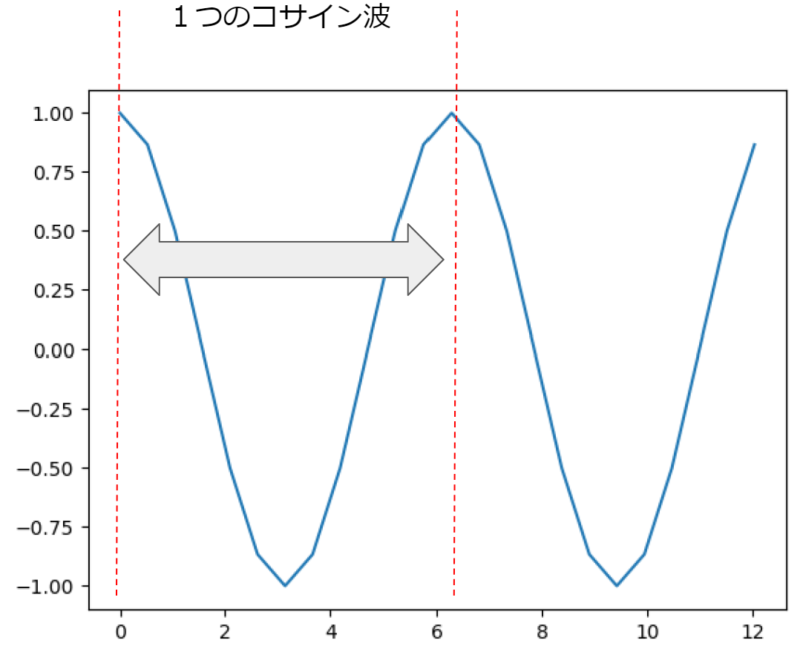
この矢印の波が、1つのコサインの波になっています。普通にcos(0°)からcos(360°)までをグラフにしたものです。
1秒間にこのコサイン波が1個あれば、その波の周波数は1Hz(ヘルツ)といいます。
1秒間に10個波があれば周波数10Hz(ヘルツ)といいます。
コサインのグラフを書いたときに、横軸は °(度)でしたが、周波数を扱うときは時間(t)になります。
周波数 n のコサイン波は式で、
cos(2πnt)
と書けます。(π:円周率、n:周波数、t:時間)
例えば、周波数1のコサイン波を考えた場合、1秒後に360°(2πラジアン)回転していればいいので、cos(at) (a:何かわからない定数、t:時間)と置くと、t=1のポイントで、
at=2π ,t=1から a=2π
なので、周波数1Hzのコサイン波は cos(2πt)になります。
例をもう一つ。周波数3Hzのコサイン波は、t=1(秒)で3回転していればいいので、360°(2π(rad))が3つなので、2π×3(rad)回転していればいいです。
なので、at=a=2π×3となり、周波数3Hzのコサイン波は cos(2π×3×t)になります。



コメント